Παραθέτω από πραγματική προσομοίωση της λύσης:
(#αρ. πεντάδας, όνομα αρχείου, χρόνος εκτέλεσης σε παρένθεση -
υποτίθεται δεν τον βλέπουμε / ξέρουμε)
Πρώτα ταξινομούμε ανά 5 αρχεία από τη λίστα των 250.
ΤΑΞΙΝΟΜΗΣΗ ΣΕ 50 ΠΕΝΤΑΔΕΣ
[#1] F001(055) - F004(179) - F003(211) - F005(397) - F002(819) -
[#2] F008(078) - F009(097) - F010(247) - F006(327) - F007(707) -
[#3] F013(104) - F015(361) - F014(404) - F011(591) - F012(699) -
[#4] F017(065) - F016(091) - F018(221) - F020(485) - F019(611) -
[#5] F021(037) - F025(053) - F022(229) - F023(551) - F024(763) -
[#6] F027(035) - F026(184) - F028(373) - F029(407) - F030(689) -
[#7] F033(069) - F035(133) - F034(309) - F032(429) - F031(727) -
[#8] F039(181) - F040(191) - F037(197) - F038(607) - F036(665) -
[#9] F041(187) - F043(305) - F044(387) - F042(734) - F045(823) -
[#10] F050(020) - F046(047) - F047(218) - F049(219) - F048(291) -
[#11] F052(080) - F054(098) - F055(152) - F053(385) - F051(687) -
[#12] F059(012) - F056(013) - F057(355) - F060(728) - F058(975) -
[#13] F065(082) - F061(153) - F064(271) - F062(367) - F063(671) -
[#14] F066(247) - F067(311) - F069(451) - F070(476) - F068(879) -
[#15] F074(033) - F071(057) - F075(481) - F073(497) - F072(679) -
[#16] F076(017) - F077(067) - F078(213) - F079(339) - F080(799) -
[#17] F082(144) - F081(379) - F085(423) - F083(427) - F084(638) -
[#18] F089(234) - F088(249) - F087(287) - F090(299) - F086(325) -
[#19] F092(149) - F091(235) - F094(267) - F095(345) - F093(447) -
[#20] F099(087) - F097(171) - F098(210) - F100(237) - F096(239) -
[#21] F105(024) - F104(167) - F102(188) - F101(428) - F103(647) -
[#22] F107(058) - F106(499) - F109(575) - F108(631) - F110(674) -
[#23] F114(023) - F111(137) - F113(216) - F115(326) - F112(475) -
[#24] F117(077) - F120(146) - F116(337) - F118(491) - F119(967) -
[#25] F124(143) - F122(161) - F125(171) - F123(341) - F121(719) -
[#26] F128(079) - F129(098) - F126(111) - F130(452) - F127(493) -
[#27] F131(022) - F134(087) - F133(178) - F132(626) - F135(710) -
[#28] F138(039) - F136(093) - F140(120) - F137(185) - F139(238) -
[#29] F145(019) - F144(048) - F142(073) - F143(265) - F141(587) -
[#30] F149(030) - F150(055) - F148(179) - F146(251) - F147(403) -
[#31] F153(044) - F154(066) - F155(100) - F151(222) - F152(281) -
[#32] F156(059) - F158(125) - F160(173) - F159(311) - F157(383) -
[#33] F161(147) - F165(239) - F162(333) - F163(439) - F164(584) -
[#34] F167(021) - F169(077) - F170(261) - F168(275) - F166(395) -
[#35] F172(099) - F175(128) - F173(167) - F174(173) - F171(743) -
[#36] F180(049) - F178(227) - F179(379) - F176(467) - F177(698) -
[#37] F183(101) - F185(131) - F184(166) - F181(227) - F182(277) -
[#38] F188(103) - F187(122) - F189(491) - F190(548) - F186(639) -
[#39] F193(103) - F195(182) - F194(405) - F191(497) - F192(659) -
[#40] F200(347) - F199(351) - F197(380) - F196(389) - F198(602) -
[#41] F202(088) - F201(173) - F205(653) - F204(839) - F203(923) -
[#42] F207(107) - F206(129) - F209(283) - F210(321) - F208(593) -
[#43] F212(038) - F211(043) - F215(297) - F213(451) - F214(875) -
[#44] F217(191) - F216(207) - F218(223) - F219(359) - F220(627) -
[#45] F221(093) - F225(105) - F223(487) - F222(662) - F224(787) -
[#46] F226(015) - F229(037) - F228(047) - F230(102) - F227(176) -
[#47] F233(119) - F231(170) - F234(368) - F232(467) - F235(991) -
[#48] F240(075) - F238(096) - F237(231) - F236(307) - F239(680) -
[#49] F245(031) - F241(227) - F243(239) - F242(425) - F244(559) -
[#50] F246(107) - F247(273) - F248(287) - F250(314) - F249(827) -
Στη συνέχεια ταξινομούμε τους νικητές των 50 πεντάδων δημιουργώντας 10 ταξινομημένες πεντάδες.
ΤΑΞΙΝΟΜΗΣΗ ΣΕ 10 ΠΕΝΤΑΔΕΣ
[#1] F021(037) - F001(055) - F017(065) - F008(078) - F013(104)
[#2] F050(020) - F027(035) - F033(069) - F039(181) - F041(187)
[#3] F059(012) - F074(033) - F052(080) - F065(082) - F066(247)
[#4] F076(017) - F099(087) - F082(144) - F092(149) - F089(234)
[#5] F114(023) - F105(024) - F107(058) - F117(077) - F124(143)
[#6] F145(019) - F131(022) - F149(030) - F138(039) - F128(079)
[#7] F167(021) - F153(044) - F156(059) - F172(099) - F161(147)
[#8] F180(049) - F183(101) - F193(103) - F188(103) - F200(347)
[#9] F212(038) - F202(088) - F221(093) - F207(107) - F217(191)
[#10] F226(015) - F245(031) - F240(075) - F246(107) - F233(119)
Από τους νικητές των 10 πεντάδων δημιουργούμε 2 νέες ταξινομημένες πεντάδες.
ΤΑΞΙΝΟΜΗΣΗ ΣΕ 2 ΠΕΝΤΑΔΕΣ
[#1] F059(012) - F076(017) - F050(020) - F114(023) - F021(037)
[#2] F226(015) - F145(019) - F167(021) - F212(038) - F180(049)
Για να βρούμε το νικητή (το πιο γρήγορο αρχείο όλων) ταξινομούμε τους νικητές των 2 παραπάνω πεντάδων.
Συμπεριλαμβάνουμε στην τελευταία αυτή εκτέλεση και τα αρχεία της δεύτερης στήλης καθώς και ένα από την τρίτη στήλη.
ΤΑΞΙΝΟΜΗΣΗ ΣΕ 1 ΠΕΝΤΑΔA
[#1]
F059(012) - F226(015) - F076(017) - F145(019) - F050(020)
Αφού ολοκληρώσουμε την παραπάνω διαδικασία βρίσκουμε το
νικητή όλων:
F059(012)
Λαμβάνουμε τώρα από τη φάση των 50 πεντάδων: την πεντάδα του νικητή, τις πεντάδες που είναι πρώτα όσα έχουμε στην τελευταία εκτέλεση και του αρχείου της τρίτης στήλης από τη φάση των 2 πεντάδων που δεν συμπεριλάβαμε πριν [F167].
Με βάση τα αποτελέσματα των τελευταίων εκτελέσεων μπορούμε να τις ταξινομήσουμε ως προς τον πρώτο της κάθε πεντάδας σε σχέση με τον πρώτο των άλλων πεντάδων (εκτός από τις δύο τελευταίες που δεν ξέρουμε τη σειρά τους):
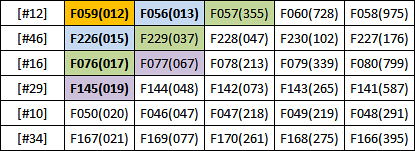
Γνωρίζουμε ότι το F226 είναι μεγαλύτερο από το F059 και δεν υπάρχει άλλο από την πρώτη στήλη μεταξύ τους. Το μόνο από τη δεύτερη στήλη που μπορεί να είναι στη δεύτερη θέση, είναι το F056.
Το F229 π.χ. δεν μπορεί να είναι, επειδή θα μεσολαβούσε το F226 που είναι μικρότερό του αλλά και μεγαλύτερο του F059.
Οπότε πρέπει να συγκρίνουμε τα F056 - F226. Όποιο είναι μικρότερο θα είναι στη δεύτερη θέση.
Για την τρίτη θέση υποψήφια είναι τα F057, F229 και F076.
Εκτελούμε τη σύγκριση όλων μαζί των παραπάνω:
[#1] F056(013) - F226(015) - F076(017) - F229(037) - F057(355)
Βρίσκουμε ότι το F056 είναι στη δεύτερη θέση.
Επομένως στην τρίτη θέση θα είναι το μικρότερο των F057 και F226. Είναι το F226.
Για την τέταρτη θέση υποψήφια είναι τα: F229 - F076. Το F060 δεν μπορεί να είναι αφού τότε το F057 θα ήταν τρίτο, πράγμα που δεν ισχύει.
Έχουμε βρει ήδη ότι το F076 είναι μικρότερο του F229, οπότε το F076 είναι στην τέταρτη θέση.
Στην πέμπτη θέση μπορεί να είναι τα: F229 - F077 - F145.
Κάνουμε τη σύγκριση και βρίσκουμε ότι στην πέμπτη θέση είναι το F145.
[#1] F145(019) - F229(037) - F077(067)
Σύνολο εκτελέσεων για τα πέντε πρώτα: 65
Μέχρι εδώ έφτασα. Δεν είμαι σίγουρος αν καλύπτει όλες τις περιπτώσεις.

