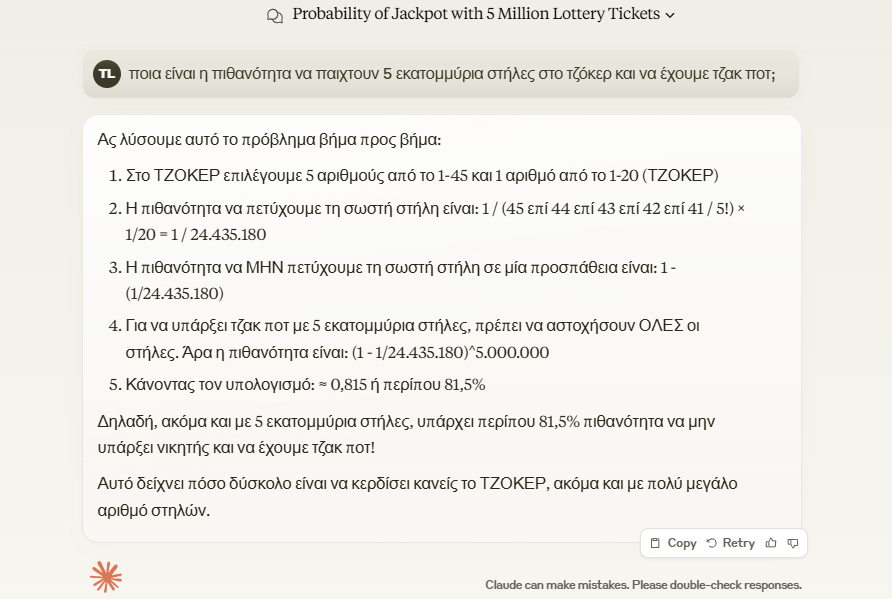
Τα τυχερά παιχνίδια είναι στημένα

[Crimson_2]

Αναμενόμενο. Έκαστος στο είδος του.

[nik_killthemall]

SpoilerShow

Υπό τη συνθήκη n=m. Αν n<m, δεν νομίζω.

Οπότε λέμε:

n: πλήθος διακριτών στηλών
m: πλήθος όλων των στηλών που παίχτηκαν
k: πλήθος όλων των δυνατών στηλών του παιχνιδιού = 24_435_180

Εγώ ισχυρίζομαι πως η πιθανότητα να βρεθεί νικητής δίνεται από τον τύπο n/k, και είναι ανεξάρτητη από το m.

Εσύ τι λες;

Σωστή προσέγγιση είναι, αλλά δείξε μου πώς βρίσκεις τις n διακριτές στήλες από το σύνολο m.

(Ποια η πιθανότητα οι m στήλες να προέρχονται από n διακριτές)

Θα προχωρήσω λίγο σε αυτή την προσέγγιση. Θα βάλω σύμβολο ν=24435180 το πλήθος όλων των δυνατών στηλών του παιχνιδιού, γιατί θα χρησιμοποιήσω αλλιώς τα k. Επίσης για το πλήθος των διακριτών στοιχείων θα χρησιμοποιήσω το s.

Μ είναι η λίστα όλων των παιγμένων στηλών μιας κλήρωσης τζόκερ, που έχει πλήθος m. Περιλαμβάνει κάποια στοιχεία από όλο τον "χώρο" των στηλών {1, ..., ν} που επαναλαμβάνονται. Αν μια στήλη i ανήκει στη λίστα Μ, θα επαναλαμβάνεται k_i>0 φορές (μία, δυο, τρεις κλπ). Αν η στήλη i δεν βρίσκεται στη λίστα Μ θα έχουμε συμβατικά k_i=0. Με άλλα λόγια για κάθε στοιχείο από όλες τις δυνατές στήλες φτιάχνουμε έναν αριθμό (ας τον πούμε πολλαπλότητα ή δείκτη επανάληψης, στη λίστα M).

Το ενδιαφέρον αυτών των αριθμών είναι:
(1) ότι είναι ακέραιοι θετικοί ή μηδέν
(2) k₁+...+k_v=m (v=24435180, το m γνωστοποιείται σε κάθε κλήρωση)
(3) Αυτοί που είναι μηδέν, μας βοηθούν για να βρεθούν οι s διακριτές στήλες από τη λίστα των m στοιχείων.

Το πρόβλημα είναι ότι δεν ξέρουμε πόσοι και ποιοι είναι οι συγκεκριμένοι δείκτες, θα πιθανολογήσουμε απαριθμώντας τις ακέραιες λύσεις γραμμικής εξίσωσης που είναι στο (2). Η απαρίθμηση ακολουθεί τους τρόπους να κατανείμεις m αντικείμενα σε ν δοχεία, επιτρέποντας να μείνουν άδεια δοχεία.

Αν έχω μεταφέρει σωστά τον τύπο, τότε η πιθανότητα το k_i να είναι μηδέν, δηλαδή ότι η στήλη i δεν ανήκει στη λίστα των παιγμένων, είναι:

p=P(k_i=0)=(ν-1)/(m+v-1)

Ενώ η στήλη έχει πολλαπλότητα k_i>0 με πιθανότητα 1-p και επομένως ανήκει στις διακριτές στήλες της λίστας.

Αυτό δηλαδή σημαίνει ότι έχω μια υπολογισμένη πιθανότητα επιτυχούς δοκιμής Bernoulli, με την οποία μπορώ να "σαρώσω" μία-μία, κάθε στήλη i από τον χώρο των δυνατών στηλών και να βρω πιθανότητα να ανήκει στη λίστα. Με τις γνωστές ενστάσεις περί ανεξαρτησίας των δοκιμών, έχω ν δοκιμές Bernoulli, δηλαδή διωνυμική κατανομή.

Prob{ο αριθμός διακριτών στηλών της λίστας των παιγμένων είναι ακριβώς s} = C(v,s)*(m/m+v-1)^s * (v-1/m+v-1)^(v-s)

(όπου C(v,k) το πλήθος συνδυασμών ν ανά k)

Και από εκεί και πέρα μπορούμε να φτιάξουμε πιθανότητες για την εύρεση νικητή στη βάση του τύπου: Prob{υπάρχει νικητής}=s/v

Εκτός του s έχουμε όλες τις άλλες ποσότητες γνωστές, σχετικά απλοί τύποι στον υπολογισμό, αλλά δεν θα βάλω ακόμη αριθμούς. Το ποστ γράφτηκε με κάποιο ενθουσιασμό της ανεύρεσης: μπορεί όλο το σκεπτικό να βγαίνει λάθος, μπορεί να έχω επιμέρους λάθη, αλλά τελοσπάντων, απλά το δείχνω.

(kudos σε pussycat)

Αν καταλαβαινω καλα αποδιδεις μια πολλαπλοτητα εμφανισης σε καθε συνδυασμο του τζοκερ ! (μηδεν πολλαπλοτητα η μη εμφανιση).

1) Σε πρωτη φαση δεν πιανω γιατι η πιθανοτητα ki = 0, δηλ η πιθανοτητα μη εμφανισης καποιας στηλης, ειναι ιση με (ν-1)/(m+v-1). Μπορεις να εξηγησεις με ποιο σκεπτικο βγαζεις αυτον τον τυπο ?

Ας πουμε εγω εκει θα εβαζα τον τυπο (ν-m) / ν, δηλ. ποσοι δεν εμφανιστηκαν προς ποσοι ειναι συνολικα οι συνδυασμοι, με το σκεπτικο πως ο δειγματικος χωρος εχει πληθος ν=24435180 και οποιοδηποτε συνολο κι αν ορισουμε πρεπει να ειναι υποσυνολο αυτου του δειγματικου χωρου.

2) Αν καταλαβαινω καλα, θεωρεις πως εκτελεις το εξης πειραμα τυχης : Παιρνεις τυχαια μια στηλη του δειγματικου χωρου και βλεπεις αν αυτη βρισκεται μεσα στις παιγμενες στηλες (αποτυχια 1-p) ή οχι (επιτυχια p) της κληρωσης.
Στον τυπο αυτο C(v,s)*(m/m+v-1)^s * (v-1/m+v-1)^(v-s) της διωνυμικης, καταλαβαινω οτι το ν ειναι οι επαναληψεις του πειραματος σου και το s ειναι το ποσες φορες θελεις στις ν επαναληψεις να ερθει επιτυχια, δηλ, μη εμφανιση στους παιγμενους (αυτην εχεις ορισει ως επιτυχια).
Ετσι αν s=1 υπολογιζεις την πιθανοτητα σε ν=24435180 επαναληψεις του πειραματος σου να εμφανιστει επιτυχια s=1 μια φορα, επιτυχια ομως για σενα ειναι η μη εμφανιση στηλης μεσα στις παιγμενες να συμβει 1 φορα, αρα τις υπολοιπες 24435180 - 1 φορες εκτελεσης του πειραματος σου θελεις να εχεις αποτυχια δηλ. εμφανιση στηλης μεσα στις παιγμενες !

Μεχρι εδω το εχω καταλαβει καλα ?

[nik_killthemall]

κοτας, μαγκια σου, οποτε παρε πουλο και μην μας πρηζεις ταρχιδια.

(ξερεις εσυ)

[Ανίκητος]

@nik_killthemall

Παράδειγμα μιας λίστας με 48 εκατομμύρια παιγμένες στήλες θα βρεις εκεί:
Ανίκητος @ Τα τυχερά παιχνίδια είναι στημένα

- Σε κάθε κλήρωση ξέρεις το m, που μπορεί να είναι 5 ή 48 εκατομμύρια, οσεσδήποτε παιγμένες στήλες.
- Δεν ξέρεις πόσες διακριτές στήλες έχει η λίστα με τις παιγμένες, το συμβολίζω s και είναι s≤v.
- Κάθε στήλη i από όλες τις δυνατές v, ή δεν θα έχει παιχτεί (k_i=0), ή θα έχει παιχτεί k_i φορές. Όχι απαραίτητα από τον ίδιο παίκτη.
- Άρα m=k₁+...+k_v, δηλαδή ακέραιες λύσεις γραμμικής εξίσωσης. Έχει συγκεκριμένο τύπο για το πόσες υπάρχουν.
- Τον τύπο τον μετέφερα από βιβλίο, οπότε μπορεί και να έχω αντικαταστήσει λάθος τα σύμβολα. Δεν προφταίνω να τον ελέγξω.
- Από όλα τα k_i, (v-s) είναι μηδέν. Άρα ο τύπος απαριθμεί τρόπους (v-s) μηδενικών σε ν προσθετέους (με άθροισμα m).
- Από αυτό προκύπτουν πιθανότητες P{k_i>0}, P{k_i=0} δηλαδή αν ανήκει ή όχι στη λίστα των m παιγμένων στηλών.
- Αποκαλώ την μια την πιθανότητα "επιτυχίας", για να υπολογίσω με διωνυμική με v δοκιμές την πιθανότητα για την τιμή του s.
- Σκασίλα μου αν εσύ θεωρείς πως δεν μπορώ να πάρω διωνυμική αφού κατά την αποψάρα σου δεν είναι ανεξάρτητες οι δοκιμές.
- Εκκρεμεί να υπολογίσω πιθανότητα του νικητή βάσει του τύπου s/ν, μόνο που τώρα έχουμε μια κατανομή πιθανοτήτων για το s.
- Θα είναι ένας ακόμη "λάθος τύπος" άλλωστε, γιατί αν δεν πάρουμε ανεξάρτητους παίκτες, πέφτει μπούλινγκ.

Όποιος θέλει να καταλάβει, καταλαβαίνει.

[Ανίκητος]

και το claude ai θέλει δουλειά.

Θέλει. Αφού δεν έχει αποδείξει μαθηματικά την ανεξαρτησία δυο ενδεχομένων, όταν αυτά είναι απλά ενδεχόμενα.

[nik_killthemall]

- Σκασίλα μου αν εσύ θεωρείς πως δεν μπορώ να πάρω διωνυμική αφού κατά την αποψάρα σου δεν είναι ανεξάρτητες οι δοκιμές.

Πας καλα ρε μπαγλαμα ? Που ακριβως εγραψα οτι δεν μπορεις να παρεις διωνυμικη κατανομη ? Οι στηλες δεν ειναι ανεξαρτητες δοκιμες για το πειραμα που λεγεται κληρωση τζοκερ που γινεται καθε τριτη, πεμπτη και κυριακη !
Εσυ σε ολο τον συλλογισμο δεν εγραψες πουθενα για αυτο το πειραμα ... Βασικα δεν εγραψες καν ποιο ειναι το πειραμα σου στο οποιο χρησιμοποιεις την διωνυμικη, και ρωτησα ποιο ειναι αυτο το πειραμα τις διωνυμικης που κανεις ?

Αφιερωσα 10 λεπτα να διαβασω αυτο που εγραψες και εκανα με καλη προθεση 2 διευκρινιστικες ερωτησεις και η απαντηση σου ειναι αυτο ?

Βρε ουστ ζουδι

Ας εγραφες οτι απευθυνεσαι με αυτο που εγραψες σε ολους εκτον απο τον κιλ, για να βγαλω τον σκασμο.

σκαω και κανω χωρο στα μιλιουνια του λαου να ασχοληθουν με τα οσα εγραψες

[Ανίκητος]

Πας καλα ρε μπαγλαμα ? Που ακριβως εγραψα οτι δεν μπορεις να παρεις διωνυμικη κατανομη ? Οι στηλες δεν ειναι ανεξαρτητες δοκιμες για το πειραμα που λεγεται κληρωση τζοκερ που γινεται καθε τριτη, πεμπτη και κυριακη !
Εσυ σε ολο τον συλλογισμο δεν εγραψες πουθενα για αυτο το πειραμα ... Βασικα δεν εγραψες καν ποιο ειναι το πειραμα σου στο οποιο χρησιμοποιεις την διωνυμικη, και ρωτησα ποιο ειναι αυτο το πειραμα τις διωνυμικης που κανεις ?

Έγραψα για την δοκιμή Bernoulli όμως ποια είναι και την εφαρμόζω ν φορές στο σύνολο {1,...,ν} όλων των δυνατών στηλών.
Η i στήλη του συνόλου {1,...,ν} έχει αριθμό k_i επαναλήψεων στη λίστα Μ των παιγμένων στηλών.
Αυτό το k_i έχει πιθανότητα p να είναι 0 (δεν ανήκει στη Μ) ή 1-p ώστε η στήλη i να επαναλαμβάνεται 1, 2, 3 κλπ. (χωρίς όριο) φορές στη λίστα Μ.
Η διωνυμική είναι η B(ν,p). Δεν ξέρω τι άλλο χρειάζεσαι για να έχεις εικόνα του πειράματος.

Και για να σ' το πω ευθέως, δεν γίνεται να μου πεις ότι οι δοκιμές αυτές είναι ανεξάρτητες (το προκαταλαμβάνω, ναι, γιατί διάβασα αρκετά από τα ποστ σου), αλλά όταν πρόκειται για τον τύπο του μπακάλη να μπορείς να λες ότι τα ενδεχόμενα δεν είναι ανεξάρτητα. Για τον ίδιο λόγο, ή θα είναι και οι δύο τύποι λάθος, ή θα βρεις άλλον λόγο να απορρίψεις τον έναν, αυτόν που σου μυρίζει.

[pussycat]

Ο παραπάνω τύπος λέει υποθέτει "random independent draws with replacement", για μένα το σημαντικό είναι τo with replacement, με επανάληψη και όχι το ανεξάρτητο, βασικά έτσι το κατάλαβα καλύτερα.

Ας πούμε πως έχουμε έναν και μόνο έναν παίκτη στην επόμενη κλήρωση του τζόκερ που παίζει 1000 στήλες. Ας πούμε πως το δοκιμάζει ο οπαπ και το έχει κλειστό για το κοινό. Αν κουμπώσουμε n=1000 στον παραπάνω τύπο, τότε η πιθανότητα που θα μας βγάλει θα είναι λάθος, γιατί στον τρόπο υπολογισμού, από τις 1000 στήλες, κάποιες από αυτές μπορεί να εμφανίζονται πάνω από 1 φορά. Το λέει: "meaning the same combination could theoretically be picked more than once".

Βέβαια, υποτίθεται πως στις 1000 στήλες που έπαιξε ο παίκτης, όλες ήταν διακριτές. Οπότε ΑΝ όλες οι 1000 ήταν διακριτές, ο τύπος είναι θεωρητικά λάθος. Αν όμως στις 1000 στήλες του είχε και 2πλες, 3πλες κλπ μέσα, τότε είναι σωστός, διότι όπως ο τύπος αφήνει τις πολλαπλές στήλες, με τον ίδιο τρόπο έπαιξε και ο παίκτης (με πολλαπλές στήλες).

Οπότε δεν έχει να κάνει τόσο με τους παίκτες, από τη στιγμή που είδαμε πως και με έναν μόνο παίκτη ο τύπος είναι προβληματικός, αλλά με το γεγονός ότι το τζόκερ δεν αφήνει τον ίδιο παίκτη να παίξει την ίδια στήλη παραπάνω από μια φορά.

Αλλά και αυτό δεν είναι και τόσο ακριβές: το τζόκερ μπορεί και να τον αφήνει να παίξει την ίδια στήλη πάνω από μια φορά για να του πάρει τα λεφτά, αλλά όταν θα πάει ταμείο, δε θα τον πληρώσει τόσες φορές όσες το στοίχημα που έβαλε στη στήλη του. Χε, δε νομίζω δηλαδή.

Ας πούμε πως παίζω εγώ τη στήλη Α 9 φορές, με 1 ευρω τη στήλη, δίνω 9 ευρω. Το ίδιο κάνει και ο νικ με μια στήλη όμως. Αν έρθει η στήλη Α, τότε τι θα γίνει; Θα πει το σύστημα, α έχω 9+1=10 νικητές, οπότε εγώ θα πάρω το 90% του τζόκερ και ο νικ το 10%; Ή θα τα μοιραστούμε;

Και αν η απάντηση στο παραπάνω φαίνεται αυτονόητη (θα πάρω εγώ το 90% χεχε), ίσως δεν είναι και τόσο όταν παίζονται συστήματα. Δλδ όταν τη νικητήρια στήλη Α την έπιασα όχι γιατί την έπαιξα βλακωδώς απομονωμένα 9 φορές, αλλά γιατί επαναλήφθηκε 9 φορές ως μέρος των διαφορετικών συστημάτων μου. πχ σύστημα 1 με 7 νούμερα, σύστημα 2 με 10 νούμερα κλπ. Και αν πει κανείς, οκ είναι το τζόκερ, δε θα το πάρεις όσες φορές και να το έβαλες, τι γίνεται με τις μικρότερες νίκες, πχ 3αρια, 4ρια, 3+1 κλπ; Και πάλι δε θα πρέπει το παιχνίδι να με λογίζει μόνο μια φορά; Ή θα πρέπει να με ανταμείβει γιατί έπιασα το 3αρι αρκετές φορές μέσω του συστήματός μου; Και αν ναι, πόσες

Ανίκητε, νομίζω κάτι σημαντικό έχεις γράψει, αλλά δεν έχω χρόνο τώρα να το επεξεργαστώ, θα σας ενημερώσω!

[axilmar]

Το τζοκερ παιζεται σε επιπεδο στηλων, οχι παιχτων.

Εαν μια στηλη επαναλαμβανεται 10 φορες, και βγει νικητρια, το επαθλο θα μοιραστει στα 10.

Το ποιοι παιξανε τις 10 στηλες ειναι αδιαφορο. Μπορει να τα παρει ενας, δεκα, ή κατι ενδιαμεσο, αναλογα με το πως εχει παιχτει.

[Yochanan]

Διάβασα με προσοχή τα ποστ στο παρόν νήμα και για να κλείσει το θέμα θα γράψω το εξης:

Biceps size: 43cm.

Κέρδισα. Γεια σας.

[pussycat]

Το τζοκερ παιζεται σε επιπεδο στηλων, οχι παιχτων.

Εαν μια στηλη επαναλαμβανεται 10 φορες, και βγει νικητρια, το επαθλο θα μοιραστει στα 10.

Το ποιοι παιξανε τις 10 στηλες ειναι αδιαφορο. Μπορει να τα παρει ενας, δεκα, ή κατι ενδιαμεσο, αναλογα με το πως εχει παιχτει.

Και εδώ τι γίνεται;

Ας πούμε πως παίζω εγώ τη στήλη Α 9 φορές, με 1 ευρω τη στήλη, δίνω 9 ευρω. Το ίδιο κάνει και ο νικ με μια στήλη όμως. Αν έρθει η στήλη Α, τότε τι θα γίνει; Θα πει το σύστημα, α έχω 9+1=10 νικητές, οπότε εγώ θα πάρω το 90% του τζόκερ και ο νικ το 10%; Ή θα τα μοιραστούμε;

[Yochanan]

Και γράφοντας αυτό πήρα και 3cm στο μήκος - μόνο και που το έγραψα. Καταπληκτικά παραγωγική ημέρα σήμερα και μόλις άρχισε.

[axilmar]

Το τζοκερ παιζεται σε επιπεδο στηλων, οχι παιχτων.

Εαν μια στηλη επαναλαμβανεται 10 φορες, και βγει νικητρια, το επαθλο θα μοιραστει στα 10.

Το ποιοι παιξανε τις 10 στηλες ειναι αδιαφορο. Μπορει να τα παρει ενας, δεκα, ή κατι ενδιαμεσο, αναλογα με το πως εχει παιχτει.

Και εδώ τι γίνεται;

Ας πούμε πως παίζω εγώ τη στήλη Α 9 φορές, με 1 ευρω τη στήλη, δίνω 9 ευρω. Το ίδιο κάνει και ο νικ με μια στήλη όμως. Αν έρθει η στήλη Α, τότε τι θα γίνει; Θα πει το σύστημα, α έχω 9+1=10 νικητές, οπότε εγώ θα πάρω το 90% του τζόκερ και ο νικ το 10%; Ή θα τα μοιραστούμε;

Εσυ θα παρεις το 90% και ο νικ το 10%.

[Πασιφάη]

Είπα να κάνω μια γκεστ εμφάνιση στο νήμα κι ας μην έχω καταλάβει γρι απ'όσα γράφετε.
Είδα και το παλιογάτσουλο τον Γιοχάναν απο πάνω..Καλημέρα!

[pussycat]

Το τζοκερ παιζεται σε επιπεδο στηλων, οχι παιχτων.

Εαν μια στηλη επαναλαμβανεται 10 φορες, και βγει νικητρια, το επαθλο θα μοιραστει στα 10.

Το ποιοι παιξανε τις 10 στηλες ειναι αδιαφορο. Μπορει να τα παρει ενας, δεκα, ή κατι ενδιαμεσο, αναλογα με το πως εχει παιχτει.

Και εδώ τι γίνεται;

Ας πούμε πως παίζω εγώ τη στήλη Α 9 φορές, με 1 ευρω τη στήλη, δίνω 9 ευρω. Το ίδιο κάνει και ο νικ με μια στήλη όμως. Αν έρθει η στήλη Α, τότε τι θα γίνει; Θα πει το σύστημα, α έχω 9+1=10 νικητές, οπότε εγώ θα πάρω το 90% του τζόκερ και ο νικ το 10%; Ή θα τα μοιραστούμε;

Εσυ θα παρεις το 90% και ο νικ το 10%.

Α ναι ε; Κοίτα να δεις κάτι πράγματα, κι εγώ το έγραψα για πλάκα!