Τα τυχερά παιχνίδια είναι στημένα

[Σέλευκας]

Αυτά που είναι στημένα είναι τα τηλεοπτικά. Στον εκατομμυριούχο πρέπει να έχεις δελτίο βαριάς καθυστέρησης για να παίξεις.
Ενας τελευταίος απο το τσέισερ θα απαντούσε όλες τις ερωτήσεις όσο και να έπαιζε αλλά φαίνεται οτι δεν του αρέσει ο Αρναβούτογλου και δεν χρειάζεται και λεφτά, είναι άπλες όλοι.

[Ανίκητος]

Προφανως και δεν υπαρχει ελπιδα αλληλεπιδρασης ...

Απλα να σε ενημερωσω ( και αυτος ειναι λογος που ρωτησα 2 φορες ποιο ειναι το πειραμα τυχης στον συλλογισμο σου, αλλα και 102 να ρωτησω απαντηση δεν θα μου δωσεις εξαιτιας της αποψαρας μου και τα ρεστα) ...

Είναι ν δοκιμές Bernoulli, με πιθανότητα επιτυχίας p, που παίρνεις την στήλη i από το σύνολο όλων των δυνατών στηλών {1,...,ν} και δοκιμάζεις το ενδεχόμενο επιτυχίας k_i>0 που εκφράζει ότι η στήλη i έχει παιχτεί k_i>0 φορές στη λίστα των παιγμένων Μ.

να σε ενημερωσω λοιπον πως η διωνυμικη κατανομη αναφερεται σε πειραματα με εκβαση με δυο μονο ενδεχομενα : αποτυχια - επιτυχια, και σου υπολογιζει ποια ειναι η πιθανοτητα σε ν επαναληψεις του πειραματος η επιτυχης εκβαση να ερθει s-φορές, ΟΤΑΝ η πιθανοτητα επιτυχιας καθε μια φορα που εκτελεις το πειραμα ειναι ΣΤΑΘΕΡΗ και ιση με p !

Επομένως οι s επιτυχίες δηλώνουν πόσες είναι οι διακριτές στήλες στην λίστα Μ. Οπότε το χρησιμοποιείς στον τύπο εύρεσης νικητή, s/ν.

Στο δικο σου πειραμα, που αρνεισαι να μας πεις ποιο ειναι, η πιθανοτητα επιτυχιας που ορισες (και παλι αρνεισαι να μας πεις το σκεπτικο που την ορισες τοσο) ειναι p=(ν-1)/(m+v-1)

Έχεις δίκιο στο σκεπτικό "ορισμού" της πιθανότητας.

Προέρχεται από την απαρίθμηση των ακέραιων λύσεων της γραμμικής εξίσωσης k₁+...+k_v=m. Πήρα έτοιμο τον τύπο και αντικατέστησα τα σύμβολα και έχει μόνο τα m, v, που είναι γνωστά σε κάθε κλήρωση.

Ο αριθμός μη αρνητικών ακέραιων λύσεων της γραμμικής εξίσωσης x_1+x_2+...+x_ν=κ με κ μη αρνητικό ακέραιο, είναι ίσος με C(ν+κ-1,κ)

Αντιμετωπίζει τους ν προσθετέους σαν "δοχεία" στα οποία μοιράζεται το άθροισμα, επιτρέποντας περιπτώσεις να μείνουν "άδεια", δηλαδή μηδέν.

Απαριθμείς πρώτα με πόσους δυνατούς διαφορετικούς τρόπους μπορούν να "γεμίσουν" με τιμές τα k₁, ..., k_v ώστε να ικανοποιούν την εξίσωση. Απαριθμείς κατόπιν με πόσους διαφορετικούς τρόπους γίνεται τουλάχιστον ένα από τα k₁, ..., k_v να παραμείνει μηδέν (παίρνεις μόνο ν-1 προσθετέους και το ίδιο άθροισμα και εφαρμόζεις τον τύπο). Το τελευταίο είναι ο αριθμητής και το πρώτο ο παρονομαστής για τον υπολογισμό της πιθανότητας p.

εχει μεσα δηλ το m που ειναι το πληθος παιγμενων στηλων σε καθε κληρωση, αρα αυτο το p ειναι διαφορετικο για καθε κληρωση, αρα ΑΝ το πειραμα σου ειναι η κληρωση τζοκερ, τοτε δεν μπορεις να χρησιμοποιησεις τη διωνυμικη, για το p που ορισες ΔΕΝ ειναι σταθερο ! Δηλ. σε καθε κληρωση ΑΛΛΑΖΕΙ !

Δεν διαφωνώ σε αυτό. Από κλήρωση σε κλήρωση αλλάζει το p, αφού αλλάζει η λίστα Μ και άρα η ομάδα των k_i.

[Crimson_2]

Συγγνώμη, αλλά δεν θα συνεχίσω το σχιζοφρενές παιχνιδάκι σου. Αξιοθρήνητο, δεν έχω να πω τίποτα άλλο.

Σελ 21 έγραψε αυτό, Σελ 26 ακόμα μας πρήζει το παπάρι με αντχομινεμ ο μπούφος μινιμαρκετάς προσωποποίηση του Dunning Kruger.

Μαθηματικά έχει να γράψει 20 σελίδες, εκεί δεν τον παιρνει.

[Feindflug]

Μιλάμε για θεμελιώδη έλλειψη κατανόησης πιθανοτήτων για να το λες αυτό:

Έστω Χ η πιθανότητα να παίξω έναν τάδε συνδυασμό. Εσύ υποστηρίζεις ότι αν παίξω δεύτερη φορά, η πιθανότητα να ξαναπαίξω τον ίδιο συνδυασμό είναι ΠΑΛΙ Χ. Δεν καταλαβαίνεις ότι είτε υπάρχει ΑΝΤΙκινητρο στο να παίξεις δύο φορές το ίδιο, είτε ΚΙΝΗΤΡΟ να παίξεις ΟΝΤΩΣ δύο φορές το ίδιο, η πιθανότητα ΔΕΝ ΕΙΝΑΙ Χ.

Τυπε, αν υπάρχει ταυτόχρονα κίνητρο και αντικίνητρο δεν αλληλοαναιρούνται;

Να μας πει την γνώμη του και ο Feindflug

Τύπε, η ανάλυση των στατιστικών ή όπως λέγεται αυτό που γίνεται εδώ, είναι από τα πιο ξενέρωτα πράγματα για εμένα.

Από την άλλη βέβαια, θέτεις ένα βαθύ φιλοσοφικό ερώτημα, πάνω στο οποίο προσωπικά ακροβατώ εδώ και πολλά χρόνια. Έχω κίνητρο για να μεγαλούργησω και να φτάσω σε Υπεράνθρωπα ύψη, ενώ ταυτόχρονα αυτομαστιγώνομαι και βυθίζομαι στα Τάρταρα της ματαιότητας και της απαισιοδοξίας.

Μήπως να παίξω ένα τζόκερ;

[enaon]

Συγγνώμη, αλλά δεν θα συνεχίσω το σχιζοφρενές παιχνιδάκι σου. Αξιοθρήνητο, δεν έχω να πω τίποτα άλλο.

Σελ 21 έγραψε αυτό, Σελ 26 ακόμα μας πρήζει το παπάρι με αντχομινεμ ο μπούφος μινιμαρκετάς προσωποποίηση του Dunning Kruger.

Μαθηματικά έχει να γράψει 20 σελίδες, εκεί δεν τον παιρνει.

και ο νικ τον εχει βαλει στο ιγνορ απο την πρώτη σελίδα νομιζω. Μην δίνεις σημασία σε λεπτομέρειες.

[nik_killthemall]

Προφανως και δεν υπαρχει ελπιδα αλληλεπιδρασης ...

Απλα να σε ενημερωσω ( και αυτος ειναι λογος που ρωτησα 2 φορες ποιο ειναι το πειραμα τυχης στον συλλογισμο σου, αλλα και 102 να ρωτησω απαντηση δεν θα μου δωσεις εξαιτιας της αποψαρας μου και τα ρεστα) ...

Είναι ν δοκιμές Bernoulli, με πιθανότητα επιτυχίας p, που παίρνεις την στήλη i από το σύνολο όλων των δυνατών στηλών {1,...,ν} και δοκιμάζεις το ενδεχόμενο επιτυχίας k_i>0 που εκφράζει ότι η στήλη i έχει παιχτεί k_i>0 φορές στη λίστα των παιγμένων Μ.

να σε ενημερωσω λοιπον πως η διωνυμικη κατανομη αναφερεται σε πειραματα με εκβαση με δυο μονο ενδεχομενα : αποτυχια - επιτυχια, και σου υπολογιζει ποια ειναι η πιθανοτητα σε ν επαναληψεις του πειραματος η επιτυχης εκβαση να ερθει s-φορές, ΟΤΑΝ η πιθανοτητα επιτυχιας καθε μια φορα που εκτελεις το πειραμα ειναι ΣΤΑΘΕΡΗ και ιση με p !

Επομένως οι s επιτυχίες δηλώνουν πόσες είναι οι διακριτές στήλες στην λίστα Μ. Οπότε το χρησιμοποιείς στον τύπο εύρεσης νικητή, s/ν.

Στο δικο σου πειραμα, που αρνεισαι να μας πεις ποιο ειναι, η πιθανοτητα επιτυχιας που ορισες (και παλι αρνεισαι να μας πεις το σκεπτικο που την ορισες τοσο) ειναι p=(ν-1)/(m+v-1)

Έχεις δίκιο στο σκεπτικό "ορισμού" της πιθανότητας.

Προέρχεται από την απαρίθμηση των ακέραιων λύσεων της γραμμικής εξίσωσης k₁+...+k_v=m. Πήρα έτοιμο τον τύπο και αντικατέστησα τα σύμβολα και έχει μόνο τα m, v, που είναι γνωστά σε κάθε κλήρωση.

Ο αριθμός μη αρνητικών ακέραιων λύσεων της γραμμικής εξίσωσης x_1+x_2+...+x_ν=κ με κ μη αρνητικό ακέραιο, είναι ίσος με C(ν+κ-1,κ)

Αντιμετωπίζει τους ν προσθετέους σαν "δοχεία" στα οποία μοιράζεται το άθροισμα, επιτρέποντας περιπτώσεις να μείνουν "άδεια", δηλαδή μηδέν.

Απαριθμείς πρώτα με πόσους δυνατούς διαφορετικούς τρόπους μπορούν να "γεμίσουν" με τιμές τα k₁, ..., k_v ώστε να ικανοποιούν την εξίσωση. Απαριθμείς κατόπιν με πόσους διαφορετικούς τρόπους γίνεται τουλάχιστον ένα από τα k₁, ..., k_v να παραμείνει μηδέν (παίρνεις μόνο ν-1 προσθετέους και το ίδιο άθροισμα και εφαρμόζεις τον τύπο). Το τελευταίο είναι ο αριθμητής και το πρώτο ο παρονομαστής για τον υπολογισμό της πιθανότητας p.

εχει μεσα δηλ το m που ειναι το πληθος παιγμενων στηλων σε καθε κληρωση, αρα αυτο το p ειναι διαφορετικο για καθε κληρωση, αρα ΑΝ το πειραμα σου ειναι η κληρωση τζοκερ, τοτε δεν μπορεις να χρησιμοποιησεις τη διωνυμικη, για το p που ορισες ΔΕΝ ειναι σταθερο ! Δηλ. σε καθε κληρωση ΑΛΛΑΖΕΙ !

Δεν διαφωνώ σε αυτό. Από κλήρωση σε κλήρωση αλλάζει το p, αφού αλλάζει η λίστα Μ και άρα η ομάδα των k_i.

Αρα το πειραμα που κανεις δεν ειναι η κληρωση του τζοκερ, αλλα μια δικια σου επαναλαμβανομενη κληρωση με εκατομμυρια επαναληψεις, που την κανεις για τις πληροφοριες (δηλ. το συνολο παιγμενων στηλων ) μιας μονο κανονικης κληρωσης. Προφανως τοτε οι δοκιμες που κανεις ειναι ανεξαρτητες γιατι μιλαμε για ξεχωριστα πειραματα και προφανως αφου η p ειναι σταθερη μπορεις να χρησιμοποιησεις διωνυμικη. (εξακολουθω και εσυ αποτι καταλαβαινω να μην κατανοουμε πως προκυπτει ο τυπος του p που παιρνεις).

Απλα δεν καταλαβαινω στο τελος ποιο ειναι το ζητουμενο για το πειραμα σου. Χρησιμοποιωντας την διωνυμικη για 24 εκ επαναληψεις του πειραματος σου, τοτε αν s=1, θα εχεις υπολογισεις την πιθανοτητα σε 24 εκ επαναληψεις να εχεις 1 φορα θετικη εκβαση στο πειραμα σου. (η θετικη εκβαση αποτι θυμαμαι ειναι το ki=0 που σημαινει συνδυασμος που δεν ειναι στις παιγμενες στηλες).

Αρα θα εχεις υπολογισει τη πιθανοτητα σε 24 εκ δοκιμες μια απο αυτες τις δοκιμες να μην δινει συνδυασμο εντος των παιγμενων στηλων.
Για s=2 τη πιθανοτητα σε 24 εκ δοκιμες 2 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
Για s=3 τη πιθανοτητα σε 24 εκ δοκιμες 3 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
κοκ

Οκ και τι τις κανεις ολες αυτες τις πιθανοτητες ?

[Ανίκητος]

Αρα το πειραμα που κανεις δεν ειναι η κληρωση του τζοκερ, αλλα μια δικια σου επαναλαμβανομενη κληρωση με εκατομμυρια επαναληψεις, που την κανεις για τις πληροφοριες (δηλ. το συνολο παιγμενων στηλων ) μιας μονο κανονικης κληρωσης. Προφανως τοτε οι δοκιμες που κανεις ειναι ανεξαρτητες γιατι μιλαμε για ξεχωριστα πειραματα και προφανως αφου η p ειναι σταθερη μπορεις να χρησιμοποιησεις διωνυμικη. (εξακολουθω και εσυ αποτι καταλαβαινω να μην κατανοουμε πως προκυπτει ο τυπος του p που παιρνεις).

Το ίδιο γίνεται και με τον άλλο τύπο "του μπακάλη" αλλά δεν το παραδέχεσαι.

Απλα δεν καταλαβαινω στο τελος ποιο ειναι το ζητουμενο για το πειραμα σου. Χρησιμοποιωντας την διωνυμικη για 24 εκ επαναληψεις του πειραματος σου, τοτε αν s=1, θα εχεις υπολογισεις την πιθανοτητα σε 24 εκ επαναληψεις να εχεις 1 φορα θετικη εκβαση στο πειραμα σου. (η θετικη εκβαση αποτι θυμαμαι ειναι το ki=0 που σημαινει συνδυασμος που δεν ειναι στις παιγμενες στηλες).

Αρα θα εχεις υπολογισει τη πιθανοτητα σε 24 εκ δοκιμες μια απο αυτες τις δοκιμες να μην δινει συνδυασμο εντος των παιγμενων στηλων.
Για s=2 τη πιθανοτητα σε 24 εκ δοκιμες 2 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
Για s=3 τη πιθανοτητα σε 24 εκ δοκιμες 3 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
κοκ

Οκ και τι τις κανεις ολες αυτες τις πιθανοτητες ?

Κατανομή.

Εσύ το είπες ότι η διωνυμική υπολογίζει ποια είναι η πιθανότητα σε ν επαναλήψεις του πειράματος η επιτυχής έκβαση να έρθει s φορές.

Το s εκφράζει τις διακριτές στήλες που υπάρχουν μέσα στη λίστα με τις παιγμένες στήλες. Άρα ξέρεις την πιθανότητα από μια λίστα m παιγμένων στηλών σε μια κλήρωση, να έχει s διακριτές στήλες. Για το m δημοσιεύεται σε κάθε κλήρωση ποια αριθμητική τιμή έχει.

Άρα ξέρεις την πιθανότητα νικητή βάσει του τύπου s/ν. Π.χ. (1/ν)E[s]

Το απρόσμενο είναι ότι η πιθανότητα p της δοκιμής προκύπτει μόνο από τις m, v, οπότε είναι σταθερή σε κάθε κλήρωση (όχι από κλήρωση σε κλήρωση όμως).

Προέκυψε από την εξίσωση k₁+...+k_v=m που την παρατήρησα με τον πίνακα που δείχνει πόσες φορές παίζεται η κάθε δυνατή στήλη, στη λίστα των παιγμένων στηλών μιας κλήρωσης.


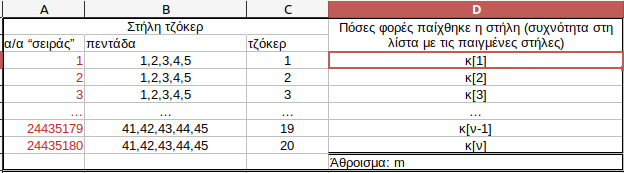
Για το πλήθος των λύσεων της εξίσωσης ανέτρεξα σε βιβλίο.

[nik_killthemall]

Αρα το πειραμα που κανεις δεν ειναι η κληρωση του τζοκερ, αλλα μια δικια σου επαναλαμβανομενη κληρωση με εκατομμυρια επαναληψεις, που την κανεις για τις πληροφοριες (δηλ. το συνολο παιγμενων στηλων ) μιας μονο κανονικης κληρωσης. Προφανως τοτε οι δοκιμες που κανεις ειναι ανεξαρτητες γιατι μιλαμε για ξεχωριστα πειραματα και προφανως αφου η p ειναι σταθερη μπορεις να χρησιμοποιησεις διωνυμικη. (εξακολουθω και εσυ αποτι καταλαβαινω να μην κατανοουμε πως προκυπτει ο τυπος του p που παιρνεις).

Το ίδιο γίνεται και με τον άλλο τύπο "του μπακάλη" αλλά δεν το παραδέχεσαι.

Δεν γινεται το ιδιο και το απεδειξα με μαθηματικα !

Η διχογνωμια δεν ειναι αν οι στηλες ειναι ανεξαρτητες ή οχι, η διχογνωμια ειναι πως

- (Α) κατα την γνωμη σας ενα τεραστιο ποσοστο παιχτων σε καθε κληρωση τζοκερ παιζουν ιδιες στηλες πληρωνοντας περισσοτερα λεφτα για τις ιδιες πιθανοτητες

- ενω (Β) κατα τη γνωμη μου το ποσοστο αυτων των παιχτων ειναι μηδενικο

Οι ΜΑΘΗΜΑΤΙΚΕΣ ΣΥΝΘΗΚΕΣ για το ποτε οι στηλες ειναι ανεξαρτητες και ποτε ειναι εξαρτημενες ειναι ΑΝΑΜΦΙΣΒΗΤΗΤΕΣ σε μια κληρωση τζοκερ ! Αν συμβαινει στη πραγματικοτητα των παιγμενων στηλων το (Α) τοτε οι στηλες ειναι εξαρτημενες, αν συμβαινει το (Β) οι στηλες ειναι ανεξαρτητες !

Αυτο που αμφισβητειται ειναι το τι συμβαινει στη πραγματικοτητα σε καθε κληρωση το Α ή το Β !

Απλα δεν καταλαβαινω στο τελος ποιο ειναι το ζητουμενο για το πειραμα σου. Χρησιμοποιωντας την διωνυμικη για 24 εκ επαναληψεις του πειραματος σου, τοτε αν s=1, θα εχεις υπολογισεις την πιθανοτητα σε 24 εκ επαναληψεις να εχεις 1 φορα θετικη εκβαση στο πειραμα σου. (η θετικη εκβαση αποτι θυμαμαι ειναι το ki=0 που σημαινει συνδυασμος που δεν ειναι στις παιγμενες στηλες).

Αρα θα εχεις υπολογισει τη πιθανοτητα σε 24 εκ δοκιμες μια απο αυτες τις δοκιμες να μην δινει συνδυασμο εντος των παιγμενων στηλων.
Για s=2 τη πιθανοτητα σε 24 εκ δοκιμες 2 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
Για s=3 τη πιθανοτητα σε 24 εκ δοκιμες 3 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
κοκ

Οκ και τι τις κανεις ολες αυτες τις πιθανοτητες ?

Κατανομή.

Εσύ το είπες ότι η διωνυμική υπολογίζει ποια είναι η πιθανότητα σε ν επαναλήψεις του πειράματος η επιτυχής έκβαση να έρθει s φορές.

Το s εκφράζει τις διακριτές στήλες που υπάρχουν μέσα στη λίστα με τις παιγμένες στήλες. Άρα ξέρεις την πιθανότητα από μια λίστα m παιγμένων στηλών σε μια κλήρωση, να έχει s διακριτές στήλες. Για το m δημοσιεύεται σε κάθε κλήρωση ποια αριθμητική τιμή έχει.

Άρα ξέρεις την πιθανότητα νικητή βάσει του τύπου s/ν. Π.χ. (1/ν)E[s]

Το απρόσμενο είναι ότι η πιθανότητα p της δοκιμής προκύπτει μόνο από τις m, v, οπότε είναι σταθερή σε κάθε κλήρωση (όχι από κλήρωση σε κλήρωση όμως).

Προέκυψε από την εξίσωση k₁+...+k_v=m που την παρατήρησα με τον πίνακα που δείχνει πόσες φορές παίζεται η κάθε δυνατή στήλη, στη λίστα των παιγμένων στηλών μιας κλήρωσης.
[img]https://i.postimg.cc/zGsMgfkK/ksni ... .png[/img]

Για το πλήθος των λύσεων της εξίσωσης ανέτρεξα σε βιβλίο.

Εξηγησε το μπολντ ? Το s στον τυπο της διωνυμικης ειναι το πληθος των επιτυχιων σε 24 εκ επαναληψεις του πειραματος σου. Απο που προκυπτει οτι αυτο το s ειναι το πληθος των διακριτων στηλων (δηλ. των διαφορετικων στηλων) εκ των παιγμενων στηλων ? Εξηγηση ?

Επισης πως ακριβως κανεις κατανομη ? Το s ειναι ο αριθμος επιτυχιων στο πειραμα σου και τον δινεις εσυ.

Επιτυχια εχεις ορισει = να μην εμφανιστει συνδυασμος σε δοκιμη του πειραματος στο που να ειναι στην στηλη των παιγμενων

Αρα αν s=100 Υπολογιζεις την πιθανοτητα P100 σε 24 εκ επαναληψεις του πειραματος σου η επιτυχης εκβαση να συμβει 100 φορες = να μην εμφανιστει εντος των παιγμενων στις 100 απο τα 24 εκ επαναληψεις.

Πως ακριβως αυτες οι πιθανοτητες σχετιζονται με τις πιθανοτητες της κληρωσης νικητη σε μια και μοναδικη κληρωση που ψαχνουμε εμεις ?

[Ανίκητος]

Η διχογνωμια δεν ειναι αν οι στηλες ειναι ανεξαρτητες ή οχι, η διχογνωμια ειναι πως
- (Α) κατα την γνωμη σας ενα τεραστιο ποσοστο παιχτων σε καθε κληρωση τζοκερ παιζουν ιδιες στηλες πληρωνοντας περισσοτερα λεφτα για τις ιδιες πιθανοτητες
- ενω (Β) κατα τη γνωμη μου το ποσοστο αυτων των παιχτων ειναι μηδενικο

Αυτό που είναι η γνώμη μου είναι ότι διαφορετικοί παίκτες παίζουν τις ίδιες στήλες.

Ένας Αθηναίος παίζει μια στήλη i = (7,13,25,28,31, τζόκερ 5) και ένας Θεσσαλονικιός παίζει την ίδια στήλη i (μου είναι αδιάφορο αν συνεννοήθηκαν ή το έκαναν ανεξάρτητα). Κι αυτό μπορεί να συμβεί με πολλούς παίκτες να παίξουν την ίδια στήλη i.
Ένας μάλιστα έπαιξε την ίδια στήλη i δυο φορές: pussycat @ Τα τυχερά παιχνίδια είναι στημένα

Επομένως αυτή η παιγμένη στήλη i θα επαναλαμβάνεται μέσα στη λίστα με τις m παιγμένες.
Πόσες φορές θα επαναλαμβάνεται; k_i>0.

Πώς εσύ βγάζεις το ποσοστό αυτό των παικτών μηδενικό;

Αν δεν παιχτεί καθόλου μια στήλη j, θέτουμε k_j=0. Οπότε k₁+...+k_v=m.

Απλα δεν καταλαβαινω στο τελος ποιο ειναι το ζητουμενο για το πειραμα σου. Χρησιμοποιωντας την διωνυμικη για 24 εκ επαναληψεις του πειραματος σου, τοτε αν s=1, θα εχεις υπολογισεις την πιθανοτητα σε 24 εκ επαναληψεις να εχεις 1 φορα θετικη εκβαση στο πειραμα σου. (η θετικη εκβαση αποτι θυμαμαι ειναι το ki=0 που σημαινει συνδυασμος που δεν ειναι στις παιγμενες στηλες).

Αρα θα εχεις υπολογισει τη πιθανοτητα σε 24 εκ δοκιμες μια απο αυτες τις δοκιμες να μην δινει συνδυασμο εντος των παιγμενων στηλων.
Για s=2 τη πιθανοτητα σε 24 εκ δοκιμες 2 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
Για s=3 τη πιθανοτητα σε 24 εκ δοκιμες 3 απο αυτες τις δοκιμες να μην δινουν συνδυασμο εντος των παιγμενων στηλων.
κοκ

Οκ και τι τις κανεις ολες αυτες τις πιθανοτητες ?

Κατανομή.

Εσύ το είπες ότι η διωνυμική υπολογίζει ποια είναι η πιθανότητα σε ν επαναλήψεις του πειράματος η επιτυχής έκβαση να έρθει s φορές.

Το s εκφράζει τις διακριτές στήλες που υπάρχουν μέσα στη λίστα με τις παιγμένες στήλες. Άρα ξέρεις την πιθανότητα από μια λίστα m παιγμένων στηλών σε μια κλήρωση, να έχει s διακριτές στήλες. Για το m δημοσιεύεται σε κάθε κλήρωση ποια αριθμητική τιμή έχει.

Άρα ξέρεις την πιθανότητα νικητή βάσει του τύπου s/ν. Π.χ. (1/ν)E[s]

Το απρόσμενο είναι ότι η πιθανότητα p της δοκιμής προκύπτει μόνο από τις m, v, οπότε είναι σταθερή σε κάθε κλήρωση (όχι από κλήρωση σε κλήρωση όμως).

Προέκυψε από την εξίσωση k₁+...+k_v=m που την παρατήρησα με τον πίνακα που δείχνει πόσες φορές παίζεται η κάθε δυνατή στήλη, στη λίστα των παιγμένων στηλών μιας κλήρωσης.
[img]https://i.postimg.cc/zGsMgfkK/ksni ... .png[/img]

Για το πλήθος των λύσεων της εξίσωσης ανέτρεξα σε βιβλίο.

Εξηγησε το μπολντ ? Το s στον τυπο της διωνυμικης ειναι το πληθος των επιτυχιων σε 24 εκ επαναληψεις του πειραματος σου. Απο που προκυπτει οτι αυτο το s ειναι το πληθος των διακριτων στηλων (δηλ. των διαφορετικων στηλων) εκ των παιγμενων στηλων ? Εξηγηση ?

Αφού καταλαβαίνεις ποιες είναι (στη λίστα των παιγμένων) οι διακριτές στήλες: Είναι οι στήλες που έχουν παιχτεί τουλάχιστον μία φορά. Τι γίνεται με μια στήλη i (από τις v) όταν έχει παιχτεί; Έχει k_i>0.

Άρα αν από το σύνολο με τους δείκτες k₁, ..., k_v μπορούσες να βρεις ποιο υποσύνολό τους δεν είναι οι μηδενικές, θα έβρισκες πόσες είναι οι διακριτές στήλες στην λίστα των παιγμένων.

Επισης πως ακριβως κανεις κατανομη ? Το s ειναι ο αριθμος επιτυχιων στο πειραμα σου και τον δινεις εσυ.

Δεν κάνω κατανομή, το s ακολουθεί τη διωνυμική κατανομή (ν,p). Δεν το είδες;

Επιτυχια εχεις ορισει = να μην εμφανιστει συνδυασμος σε δοκιμη του πειραματος στο που να ειναι στην στηλη των παιγμενων

Συγνώμη αν το είπα ανάποδα κάπου προηγουμένως, οι πιθανότητες P(k_i>0) και P(k_i=0)=1-P(k_i>0) είναι συμπληρωματικές.

Αρα αν s=100 Υπολογιζεις την πιθανοτητα P100 σε 24 εκ επαναληψεις του πειραματος σου η επιτυχης εκβαση να συμβει 100 φορες = να μην εμφανιστει εντος των παιγμενων στις 100 απο τα 24 εκ επαναληψεις.

Πως ακριβως αυτες οι πιθανοτητες σχετιζονται με τις πιθανοτητες της κληρωσης νικητη σε μια και μοναδικη κληρωση που ψαχνουμε εμεις ?

Δεν παρακολούθησες προχτές τα ποστ μου με τον @pussycat;
pussycat @ Τα τυχερά παιχνίδια είναι στημένα
pussycat @ Τα τυχερά παιχνίδια είναι στημένα

Αν ξέρουμε το πλήθος των διακριτών στηλών s ανάμεσα στις παιγμένες m, τότε η πιθανότητα νικητή είναι s/ν.

[nik_killthemall]

Η διχογνωμια δεν ειναι αν οι στηλες ειναι ανεξαρτητες ή οχι, η διχογνωμια ειναι πως
- (Α) κατα την γνωμη σας ενα τεραστιο ποσοστο παιχτων σε καθε κληρωση τζοκερ παιζουν ιδιες στηλες πληρωνοντας περισσοτερα λεφτα για τις ιδιες πιθανοτητες
- ενω (Β) κατα τη γνωμη μου το ποσοστο αυτων των παιχτων ειναι μηδενικο

Αυτό που είναι η γνώμη μου είναι ότι διαφορετικοί παίκτες παίζουν τις ίδιες στήλες.

Ένας Αθηναίος παίζει μια στήλη i = (7,13,25,28,31, τζόκερ 5) και, ανεξάρτητα από τον Αθηναίο, ένας Θεσσαλονικιός παίζει την ίδια στήλη i. Κι αυτό μπορεί να συμβεί με πολλούς παίκτες να παίξουν την ίδια στήλη i.
Ένας μάλιστα έπαιξε την ίδια στήλη i δυο φορές: pussycat @ Τα τυχερά παιχνίδια είναι στημένα

Επομένως αυτή η παιγμένη στήλη i θα επαναλαμβάνεται μέσα στη λίστα με τις m παιγμένες.
Πόσες φορές θα επαναλαμβάνεται; k_i>0.

Πώς εσύ βγάζεις το ποσοστό αυτό των παικτών μηδενικό;

Αν δεν παιχτεί καθόλου μια στήλη j, θέτουμε k_j=0. Οπότε k₁+...+k_v=m.

Καμια σχεση, οταν λεω οτι κατα τη γνωμη σας τεραστιο ποσοστο παιχτων σε καθε κληρωση τζοκερ παιζουν ιδιες στηλες πληρωνοντας περισσοτερα λεφτα για τις ιδιες πιθανοτητες, ειναι ευνοητο απο το μπολντ οτι δεν εννοω πως παιζουν τις ιδιες στηλες με αλλους παιχτες, δηλ. ιδια στηλη ο Αθηναιος με τον Σαλονικιο, αυτο ασφαλως και γινεται χωρις να πληρωνουν περισσοτερα λεφτα για τις ιδιες πιθανοτητες, !

εννοω ιδιες στηλες ΜΕ ΤΟΝ ΕΑΥΤΟ ΤΟΥΣ ! Δηλ εσεις πιστευετε (Α) πως ο αθηναιος παιζει Ο ΙΔΙΟΣ 5 ιδιες στηλες σε καθε κληρωση τζοκερ, και οτι σαν κι αυτον που παιζουν ιδιες στηλες με τον εαυτο τους ειναι ενα τεραστιο ποσοστο παιχτων τζοκερ !

Αυτη ειναι η γνωμη σας. Η γνωμη μου ειναι πως το ποσοστο τετοιων παιχτων ειναι μηδεν.

Αν συμβαινει η γνωμη σας τοτε ΝΑΙ οι στηλες ειναι ανεξαρτητες ! Αν αυτο δεν συμβαινει και συμβαινει η γνωμη μου τοτε οι στηλες ειναι εξαρτημενες !

Αυτο ακριβως το απεδειξα στο πειραμα του μαο μαο που ηταν "παιδικο" ... Στο πειραμα του μαο μαο εβγαλα εκτος δειγματικου χωρου ΜΟΝΟ τα διπλα πονταρισματα του παιχτη Z ! Τα διπλα πονταρισματα μεταξυ των παιχτων X,Y, μεταξυ των παιχτων X,Z, μεταξυ των παιχτων Y,Z, ολα καταμετρηθηκαν κανονικα ! Αρα ουδεμια σχεση εχει η ιδια στηλη μεταξυ διαφορετικων παιχτων. Μιλαμε για τη διπλη στηλη του ΙΔΙΟΥ παιχτη !

Γιαυτο σου λεω πως μονο αν πιστευεις πως στο πραγματικο τζοκερ οι παιχτες που συμπληρωνουν δελτια με ιδιες στηλες ειναι χιλιαδες,
τοτε ΕΧΕΙΣ ΔΙΚΙΟ οτι οι στηλες ειναι ανεξαρτητες και ισχυει ο τυπος του μπακαλη.


Εγω παλι πιστευω πως τα δελτια με ιδιες στηλες ειναι μηδεν ! Παιζει αν οντως το αγορασε το δελτιο ο πουσι να ειναι ο μοναδικος που εριξε 2 ιδιες στηλες στις 2,5 χιλιαδες κληρωσεις του τζοκερ που εχουν γινει !

Αρα ειναι διχογνωμια για το τι συμβαινει στη πραγματικοτητα ! Για εσας εκει εξω υπαρχουν χιλιαδες δελτια τζοκερ συμπληρωμενο το καθε δελτιο με ιδιες στηλες.

Για μενα οχι !

Κατανομή.

Εσύ το είπες ότι η διωνυμική υπολογίζει ποια είναι η πιθανότητα σε ν επαναλήψεις του πειράματος η επιτυχής έκβαση να έρθει s φορές.

Το s εκφράζει τις διακριτές στήλες που υπάρχουν μέσα στη λίστα με τις παιγμένες στήλες. Άρα ξέρεις την πιθανότητα από μια λίστα m παιγμένων στηλών σε μια κλήρωση, να έχει s διακριτές στήλες. Για το m δημοσιεύεται σε κάθε κλήρωση ποια αριθμητική τιμή έχει.

Άρα ξέρεις την πιθανότητα νικητή βάσει του τύπου s/ν. Π.χ. (1/ν)E[s]

Το απρόσμενο είναι ότι η πιθανότητα p της δοκιμής προκύπτει μόνο από τις m, v, οπότε είναι σταθερή σε κάθε κλήρωση (όχι από κλήρωση σε κλήρωση όμως).

Προέκυψε από την εξίσωση k₁+...+k_v=m που την παρατήρησα με τον πίνακα που δείχνει πόσες φορές παίζεται η κάθε δυνατή στήλη, στη λίστα των παιγμένων στηλών μιας κλήρωσης.
[img]https://i.postimg.cc/zGsMgfkK/ksni ... .png[/img]

Για το πλήθος των λύσεων της εξίσωσης ανέτρεξα σε βιβλίο.

Εξηγησε το μπολντ ? Το s στον τυπο της διωνυμικης ειναι το πληθος των επιτυχιων σε 24 εκ επαναληψεις του πειραματος σου. Απο που προκυπτει οτι αυτο το s ειναι το πληθος των διακριτων στηλων (δηλ. των διαφορετικων στηλων) εκ των παιγμενων στηλων ? Εξηγηση ?

Αφού καταλαβαίνεις ποιες είναι (στη λίστα των παιγμένων) οι διακριτές στήλες: Είναι οι στήλες που έχουν παιχτεί τουλάχιστον μία φορά. Τι γίνεται με μια στήλη i (από τις v) όταν έχει παιχτεί; Έχει k_i>0.

Άρα αν από το σύνολο με τους δείκτες k₁, ..., k_v μπορούσες να βρεις ποιο υποσύνολό τους δεν είναι οι μηδενικές, θα έβρισκες πόσες είναι οι διακριτές στήλες στην λίστα των παιγμένων.

Επισης πως ακριβως κανεις κατανομη ? Το s ειναι ο αριθμος επιτυχιων στο πειραμα σου και τον δινεις εσυ.

Δεν κάνω κατανομή, το s ακολουθεί τη διωνυμική κατανομή (ν,p). Δεν το είδες;

Επιτυχια εχεις ορισει = να μην εμφανιστει συνδυασμος σε δοκιμη του πειραματος στο που να ειναι στην στηλη των παιγμενων

Συγνώμη αν το είπα ανάποδα κάπου προηγουμένως, οι πιθανότητες P(k_i>0) και P(k_i=0)=1-P(k_i>0) είναι συμπληρωματικές.

Αρα αν s=100 Υπολογιζεις την πιθανοτητα P100 σε 24 εκ επαναληψεις του πειραματος σου η επιτυχης εκβαση να συμβει 100 φορες = να μην εμφανιστει εντος των παιγμενων στις 100 απο τα 24 εκ επαναληψεις.

Πως ακριβως αυτες οι πιθανοτητες σχετιζονται με τις πιθανοτητες της κληρωσης νικητη σε μια και μοναδικη κληρωση που ψαχνουμε εμεις ?

Δεν παρακολούθησες προχτές τα ποστ μου με τον @pussycat;
pussycat @ Τα τυχερά παιχνίδια είναι στημένα
pussycat @ Τα τυχερά παιχνίδια είναι στημένα

Αν ξέρουμε το πλήθος των διακριτών στηλών s ανάμεσα στις παιγμένες m, τότε η πιθανότητα νικητή είναι s/ν.

Μαν οταν εκανα αυτην την δηλωση στη 2η σελιδα :

Αν ξέρουμε το πλήθος των διακριτών στηλών s ανάμεσα στις παιγμένες m, τότε η πιθανότητα νικητή είναι s/ν.

ο μπακαλης μου ειπε οτι κανω λαθος και παρηγγειλε να πα να φρεσκαρω τις πιθανοτητες ...


Με αυτην την δηλωση συμφωνω, αλλα δεν ξερουμε το πληθος των διακριτων στηλων σε αυτες που παιχτηκαν. Οποτε εσυ τι λες οτι ο υπολογισμος πιθανοτοτητας της διωνυμικης σε βοηθα να βρεις αυτο το πληθος των διακριτων στηλων χωρις καν να εχεις προσβαση σε αυτες ? Αν ναι πως ?

Η διωνυμικη σου δινει μια πιθανοτητα P' = f(ν,s,m)
ν = 24 εκ
m = ο αριθμος των παιγμενων στηλων

μετα τι ? πιθανοτητα P', s ειναι αγνωστα. Για να βρεις το ενα πρεπει να υποθεσεις το αλλο.

[Ανίκητος]

εννοω ιδιες στηλες ΜΕ ΤΟΝ ΕΑΥΤΟ ΤΟΥΣ ! Δηλ εσεις πιστευετε (Α) πως ο αθηναιος παιζει Ο ΙΔΙΟΣ 5 ιδιες στηλες σε καθε κληρωση τζοκερ, και οτι σαν κι αυτον ειναι ενα τεραστιο ποσοστο παιχτων τζοκερ !
Αυτη ειναι η γνωμη σας. Η γνωμη μου ειναι πως το ποσοστο τετοιων αθηναιων ειναι μηδεν.
Αν συμβαινει η γνωμη σας τοτε ΝΑΙ οι στηλες ειναι ανεξαρτητες ! Αν αυτο δεν συμβαινει και συμβαινει η γνωμη μου τοτε οι στηλες ειναι εξαρτημενες !

Κατάλαβα τι εννοείς με την έκφραση "παίζουν ίδιες στήλες με τον εαυτό τους", αλλά δεν είναι κι η πιο καλά διατυπωμένη.

Τη δική μου γνώμη την εξέφρασα μόλις προηγουμένως και μου είναι αδιάφορο αν οι παίκτες είναι ανεξάρτητοι, ή εξαρτημένοι, συνεννοούνται, ή αν καθένας παίκτης παίζει παραπάνω ίδιες στήλες γιατί μπορεί (ο @pussycat το έκανε για πλάκα) ή για να κοροϊδέψει τον προπατζή του.

Δεν ασχολούμαι με το τι κάνουν οι παίκτες, πέρα από το τι στήλες υποβάλλουν σαν σύνολο.

Μαν οταν εκανα αυτην την δηλωση :
Αν ξέρουμε το πλήθος των διακριτών στηλών s ανάμεσα στις παιγμένες m, τότε η πιθανότητα νικητή είναι s/ν.
ο μπακαλης μου ειπε οτι κανω λαθος και παρηγγειλε να πα να φρεσκαρω τις πιθανοτητες ...

Να τις φρεσκάρεις. Εμένα με έπεισε ο @pussycat αφ' ης στιγμής μου ξεκαθάρισε μια παρεξήγηση ορολογίας.
Ο @hellegennes ας τοποθετηθεί ο ίδιος, μεγάλο παιδί είναι.

Με αυτην την δηλωση συμφωνω, αλλα δεν ξερουμε το πληθος των διακριτων στηλων σε αυτες που παιχτηκαν. Οποτε εσυ τι λες οτι ο υπολογισμος πιθανοτοτητας της διωνυμικης σε βοηθα να βρεις αυτο το πληθος των διακριτων στηλων χωρις καν να εχεις προσβαση σε αυτες ? Αν ναι πως

Η διωνυμικη σου δινει μια πιθανοτητα P' = f(ν,s,m)
ν = 24 εκ
m = ο αριθμος των παιγμενων στηλων

μετα τι ? πιθανοτητα P', s ειναι αγνωστα. Για να βρεις το ενα πρεπει να υποθεσεις το αλλο.

Θα με τρελάνεις εσύ, που με ενημέρωνες πριν για τη διωνυμική. Η P' της διωνυμικής εκφράζει την πιθανότητα οι διακριτές στήλες να είναι s. Τι πιθανότητα υπάρχει να έχω 1 εκατομμύριο διακριτές στήλες μέσα στη λίστα των m παιγμένων στηλών. P'=f(24435180,1000000,m) που το m το δημοσιεύει ο ΟΠΑΠ. Ή πάρε E[s]/ν, αν θες μια τιμή οπωσδήποτε.

Ούτε τα δικά σου ποστ δεν διαβάζεις;

[nik_killthemall]

Τη δική μου γνώμη την εξέφρασα μόλις προηγουμένως και μου είναι αδιάφορο αν οι παίκτες είναι ανεξάρτητοι, ή εξαρτημένοι, συνεννοούνται, ή αν καθένας παίκτης παίζει παραπάνω ίδιες στήλες γιατί μπορεί (ο @pussycat το έκανε για πλάκα) ή για να κοροϊδέψει τον προπατζή του.

Δεν ασχολούμαι με το τι κάνουν οι παίκτες, πέρα από το τι στήλες υποβάλλουν σαν σύνολο.

Συμφωνω οτι η διατυπωση μου δεν ηταν και η καθαροτερη, απο κει και περα ομως αυτο που λες εδω δεν ισχυει !

Ο τυπος του μπακαλη εχει για ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΥΠΟΘΕΣΗ αυτο που εδω λες οτι σου ειναι αδιαφορο : Την ανεξαρτησια των στηλων ! Αν οι στηλες δεν ειναι ανεξαρτητες τοτε απαγορευεται η πιθανοτητα τομης ενδεχομενων να σπασει σε γινομενα πιθανοτητων ωστε να δωσει τον τυπο του μπακαλη. Εδω θα σε καλεσω εγω να φρεσκαρεις τις πιθανοτητες και τι ισχυει με τα ανεξαρτητα ενδεχομενα.

Μαν οταν εκανα αυτην την δηλωση :
Αν ξέρουμε το πλήθος των διακριτών στηλών s ανάμεσα στις παιγμένες m, τότε η πιθανότητα νικητή είναι s/ν.
ο μπακαλης μου ειπε οτι κανω λαθος και παρηγγειλε να πα να φρεσκαρω τις πιθανοτητες ...

Να τις φρεσκάρεις. Εμένα με έπεισε ο @pussycat αφ' ης στιγμής μου ξεκαθάρισε μια παρεξήγηση ορολογίας.
Ο @hellegennes ας τοποθετηθεί ο ίδιος, μεγάλο παιδί είναι.

Με αυτην την δηλωση συμφωνω, αλλα δεν ξερουμε το πληθος των διακριτων στηλων σε αυτες που παιχτηκαν. Οποτε εσυ τι λες οτι ο υπολογισμος πιθανοτοτητας της διωνυμικης σε βοηθα να βρεις αυτο το πληθος των διακριτων στηλων χωρις καν να εχεις προσβαση σε αυτες ? Αν ναι πως

Η διωνυμικη σου δινει μια πιθανοτητα P' = f(ν,s,m)
ν = 24 εκ
m = ο αριθμος των παιγμενων στηλων

μετα τι ? πιθανοτητα P', s ειναι αγνωστα. Για να βρεις το ενα πρεπει να υποθεσεις το αλλο.

Θα με τρελάνεις εσύ, που με ενημέρωνες πριν για τη διωνυμική. Η P' της διωνυμικής εκφράζει την πιθανότητα οι διακριτές στήλες να είναι s. Τι πιθανότητα υπάρχει να έχω 1 εκατομμύριο διακριτές στήλες μέσα στη λίστα των m παιγμένων στηλών. P'=f(24435180,1000000,m) που το m το δημοσιεύει ο ΟΠΑΠ. Ή πάρε E[s]/ν, αν θες μια τιμή οπωσδήποτε.

Ούτε τα δικά σου ποστ δεν διαβάζεις;

εγινε εγινε θα τις φρεσκαρω κι εγω τις πιθανοτητες, απλα ρε παιδι μου αυτο για το οποιο σε επεισε ο πουσικατ δηλ για το (s/ν) και σε επεισε καπου στη σελιδα 19-20 εγω το λεω απο τη σελιδα 2 του νηματος

SpoilerShow

Να ξεκαθαρίσω εξ αρχής ότι δεν αναφέρομαι σε στημένους αγώνες αλλά σε αυτά που υποτίθεται ότι είναι μόνο τύχη, π.χ. Λόττο, Τζόκερ κλπ. Πολλά χρόνια πίσω η πιθανότητα για τζακ ποτ ήταν πολύ μικρότερη από την πιθανότητα να βγει νικητής και μάλιστα αρκετές φορές έβγαιναν περισσότεροι από ένας. Τώρα θέλεις τουλάχιστον θαύμα, τι άλλαξε άραγε, οέο; Τα μαθηματικά;

Απο που προκυπτει αυτο που λες ?

Για παραδειγμα βλεπω πως στη τελευταια κληρωση παιχτηκαν 5 εκ στηλες που για να παρουμε τη worst case ας υποθεσουμε πως ολες ειναι διαφορετικες μεταξυ τους και δεν υπαρχουν διπλες. Ολοι οι συνδυασμοι στο τζοκερ ειναι κατι πανω απο 24 εκ, οποτε οι πιθανοτητες να υπαρξει νικητης ειναι 5/24 = 21% και οι πιθανοτητες να γινει τζακ ποτ ειναι 79% !

Αν τωρα στα 5 εκ στηλες υπαρχουν και διπλες (δηλ ιδιες στηλες) τοτε το 21% μικραινει κι αλλο και το 79% ανεβαινει κι αλλο. Ενω σε προηγουμενες κληρωσεις που παιζονται πολυ λιγοτερες στηλες πχ 2 εκ η πιθανοτητα για τζακποτ παει πανω απο 90% σε καθε κληρωση.

και ενα σωμα απο ακολουθους του μπακαλη μου λεει οτι το (s/ν) ειναι λαθος ... αλλα οκ θα τις φρεσκαρω τις πιθανοτητες οπως ζητας νο μπρομπ.

Παμε παρακατω, η P' της διωνυμικης εκφραζει την πιθανοτητα που υπαρχει σε 24 εκ επαναληψεις του πειραματος σου να προκυψουν s επιτυχιες !

Εσυ τωρα πρεπει να εξηγησεις ΓΙΑΤΙ οι s επιτυχιες στο πειραμα σου σημαινουν s διακριτες στηλες μεσα στις παιγμενες ! Επιτυχια στο πειραμα σου ετσι οπως εσυ την ορισες, ειναι μια στηλη απο τις 24 εκ να μην βρισκεται μεσα στις παιγμενες στηλες αφου θα εχει πολλαπλοτητα ki = 0 !

Πως αυτο ειναι ισοδυναμο με τις διακριτες στηλες των m ? Πρεπει να το εξηγησεις γιατι δεν ειναι αυτονοητο.

[Ανίκητος]

Τη δική μου γνώμη την εξέφρασα μόλις προηγουμένως και μου είναι αδιάφορο αν οι παίκτες είναι ανεξάρτητοι, ή εξαρτημένοι, συνεννοούνται, ή αν καθένας παίκτης παίζει παραπάνω ίδιες στήλες γιατί μπορεί (ο @pussycat το έκανε για πλάκα) ή για να κοροϊδέψει τον προπατζή του.

Δεν ασχολούμαι με το τι κάνουν οι παίκτες, πέρα από το τι στήλες υποβάλλουν σαν σύνολο.

Συμφωνω οτι η διατυπωση μου δεν ηταν και η καθαροτερη, απο κει και περα ομως αυτο που λες εδω δεν ισχυει !

Ο τυπος του μπακαλη εχει για ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΥΠΟΘΕΣΗ αυτο που εδω λες οτι σου ειναι αδιαφορο : Την ανεξαρτησια των στηλων ! Αν οι στηλες δεν ειναι ανεξαρτητες τοτε απαγορευεται η πιθανοτητα τομης ενδεχομενων να σπασει σε γινομενα πιθανοτητων ωστε να δωσει τον τυπο του μπακαλη. Εδω θα σε καλεσω εγω να φρεσκαρεις τις πιθανοτητες και τι ισχυει με τα ανεξαρτητα ενδεχομενα.

Ωραία, έκανα το φρεσκάρισμά μου.

Παίρνω λοιπόν δυο διαφορετικές παιγμένες στήλες i και j και θεωρώ δυο ενδεχόμενα:
έστω A_i το ενδεχόμενο η στήλη i να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
και A_j το ενδεχόμενο η στήλη j να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
Όταν συντρέχουν και τα δύο ενδεχόμενα, τότε κάποια τρίτη στήλη, παιγμένη ή όχι, έχει κληρωθεί.
Αν συμβεί η j να μην είναι νικήτρια, πώς επηρεάζει το ενδεχόμενο η i να μην είναι ούτε αυτή νικήτρια;
Εξήγησέ μου πώς γίνεται η δεσμευμένη P(A_i|A_j) ≠ P(A_i), που είναι ο άλλος τύπος για την ανεξαρτησία.
Μεγαλώνει, ή μικραίνει η πιθανότητα του ενδεχομένου A_i, όταν συμβεί το A_j;
Ή δείξε μου ποια είναι η πιθανότητα της τομής των ενδεχομένων A_i ∩ A_j, αν δεν είναι (1-1/ν)^2.

(Μου θυμίζει την ίδια αντίληψη που παρασύρεται πολύς κόσμος, ότι έχει πολύ καιρό να κληρωθεί το τάδε νούμερο τζόκερ, άρα θα πρέπει να κληρωθεί σύντομα, προκειμένου να "εξοφλήσει" την μεροληψία των προηγούμενων κληρώσεων, να αποκαταστήσει την αμεροληψία. Αλλά η ανεξαρτησία των κληρώσεων σημαίνει το αντίθετο.)

Παμε παρακατω, η P' της διωνυμικης εκφραζει την πιθανοτητα που υπαρχει σε 24 εκ επαναληψεις του πειραματος σου να προκυψουν s επιτυχιες !

Εσυ τωρα πρεπει να εξηγησεις ΓΙΑΤΙ οι s επιτυχιες στο πειραμα σου σημαινουν s διακριτες στηλες μεσα στις παιγμενες ! Επιτυχια στο πειραμα σου ετσι οπως εσυ την ορισες, ειναι μια στηλη απο τις 24 εκ να μην βρισκεται μεσα στις παιγμενες στηλες αφου θα εχει πολλαπλοτητα ki = 0 !

Πως αυτο ειναι ισοδυναμο με τις διακριτες στηλες των m ? Πρεπει να το εξηγησεις γιατι δεν ειναι αυτονοητο.

Οι m στήλες μέσα στη λίστα με παιγμένες, μπορεί να επαναλαμβάνονται, αλλά εξακολουθεί να υπάρχει το ενδεχόμενο κάποια στήλη από τις ν=24435180 να έχει παραλειφθεί από τις παιγμένες. Και δεν εννοώ να έχει παραλειφθεί μόνο μία στήλη από τις ν, αλλά μία ή περισσότερες από τις ν. Αυτό περιορίζει τον αριθμό των διακριτών στηλών μέσα στις παιγμένες από ν σε s. Οι παιγμένες είναι m και μέσα τους υπάρχουν s διακριτές, όπου s≤v.

Έβαλα k_i=0 αν έχει παραλειφθεί η στήλη i από τις v. Μια υπο-ομάδα των k_i (i=1..ν) θα έχει πλήθος s, άθροισμα m, ενώ τα υπόλοιπα θα είναι μηδενικά. Ε το κόλπο ο κόπος είναι πώς υπεισέρχονται (v-s) μηδενικά σε v προσθετέους του αθροίσματος m.

Ε δεν ξέρω τι άλλο να πω 10 χρονών ανίψι έχω θα το καταλάβει.

[nik_killthemall]

Τη δική μου γνώμη την εξέφρασα μόλις προηγουμένως και μου είναι αδιάφορο αν οι παίκτες είναι ανεξάρτητοι, ή εξαρτημένοι, συνεννοούνται, ή αν καθένας παίκτης παίζει παραπάνω ίδιες στήλες γιατί μπορεί (ο @pussycat το έκανε για πλάκα) ή για να κοροϊδέψει τον προπατζή του.

Δεν ασχολούμαι με το τι κάνουν οι παίκτες, πέρα από το τι στήλες υποβάλλουν σαν σύνολο.

Συμφωνω οτι η διατυπωση μου δεν ηταν και η καθαροτερη, απο κει και περα ομως αυτο που λες εδω δεν ισχυει !

Ο τυπος του μπακαλη εχει για ΜΑΘΗΜΑΤΙΚΗ ΠΡΟΥΠΟΘΕΣΗ αυτο που εδω λες οτι σου ειναι αδιαφορο : Την ανεξαρτησια των στηλων ! Αν οι στηλες δεν ειναι ανεξαρτητες τοτε απαγορευεται η πιθανοτητα τομης ενδεχομενων να σπασει σε γινομενα πιθανοτητων ωστε να δωσει τον τυπο του μπακαλη. Εδω θα σε καλεσω εγω να φρεσκαρεις τις πιθανοτητες και τι ισχυει με τα ανεξαρτητα ενδεχομενα.

Ωραία, έκανα το φρεσκάρισμά μου.

Παίρνω λοιπόν δυο διαφορετικές παιγμένες στήλες i και j και θεωρώ δυο ενδεχόμενα:
έστω A_i το ενδεχόμενο η στήλη i να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
και A_j το ενδεχόμενο η στήλη j να μην κληρωθεί νικήτρια, έχει πιθανότητα 1-(1/ν)
Όταν συντρέχουν και τα δύο ενδεχόμενα, τότε κάποια τρίτη στήλη, παιγμένη ή όχι, έχει κληρωθεί.
Αν συμβεί η j να μην είναι νικήτρια, πώς επηρεάζει το ενδεχόμενο η i να μην είναι ούτε αυτή νικήτρια;
Εξήγησέ μου πώς γίνεται η δεσμευμένη P(A_i|A_j) ≠ P(A_i), που είναι ο άλλος τύπος για την ανεξαρτησία.
Μεγαλώνει, ή μικραίνει η πιθανότητα του ενδεχομένου A_i, όταν συμβεί το A_j;
Ή δείξε μου ποια είναι η πιθανότητα της τομής των ενδεχομένων A_i ∩ A_j, αν δεν είναι (1-1/ν)^2.

(Μου θυμίζει την ίδια αντίληψη που παρασύρεται πολύς κόσμος, ότι έχει πολύ καιρό να κληρωθεί το τάδε νούμερο τζόκερ, άρα θα πρέπει να κληρωθεί σύντομα, προκειμένου να "εξοφλήσει" την μεροληψία των προηγούμενων κληρώσεων, να αποκαταστήσει την αμεροληψία. Αλλά η ανεξαρτησία των κληρώσεων σημαίνει το αντίθετο.)

Στο απεδειξα αυτο που ζητας οταν ν=6 (μια ζαρια) και παιχτες = 3 ! Τοτε η πιθανοτητα ειναι (1-c1/ν)*(1-c2/ν)*(1-c3/ν) οπου c1,c2,c3 οι διαφορετικες στηλες που θα εχει παιξει ο καθε παιχτης και αυτο επειδη οι στηλες δεν θα ειναι ανεξαρτητες αλλα θα ειναι οι παιχτες !
Μπορεις να πας εδω στο σποιλερ που σου εχω δειξει καμια 30αρια φορες εως τωρα την αποδειξη και να μου αποδειξεις το λαθος ! Και μην μου πεις για παιδικα πειραματα κλπ υπαρχει κατι που λεγεται και αναδρομικη αποδειξη. (αποδειξη για ν=1, για ν=ν, για ν=ν+1), δεν χρειαζεται να παιδευεσαι με τα εκ συνδυασμων ντε και καλα.

SpoilerShow

Ορισμοι :

U = ενωση (ή)
/ = δεσμευμενη πιθανοτητα
^ = τομη (και)

Ενδεχομενο να μην πετυχει κανενας το αποτελεσμα της ζαριας = Α
Ενδεχομενο να ειναι και τα 4 πονταρισματα διαφορετικα = Β
Ενδεχομενο να ειναι ιδια μονο 2 πονταρισματα = Γ = 3 διαφορετικα πονταρισματα
Ενδεχομενο να ειναι ιδια μονο 3 πονταρισματα = Δ = 2 διαφορετικα πονταρισματα

Λύση :

Απο τη στιγμη που ο ενας απο τους τρεις πχωρουμιτες θα παιξει 2 διαφορετικα πονταρισματα και οχι ΙΔΙΑ, δεν προκειται να εμφανιστουν ΠΟΤΕ 4 ιδια πονταρισματα, οποτε ολοι οι δυνατοι συνδυασμοι των 4 πονταρισματων ΔΕΝ θα ειναι 6*6*6*6, αλλα θα ειναι (6*5)*6*6 !

Τα Β,Γ,Δ και παλι ειναι ξενα μεταξυ τους και η ενωση τους εχει πιθανοτητα 1 ! Και συγκεκριμενα :

P(Β) = (6*5*4*3)/(6*5*6*6) = 12/36 = 33.33%
P(Γ) = (6*5 *4 + 2*6*4*5 +2*6*4*5) /(6*5*6*6) = 20/36 = 55,55%
P(Δ) = (6*5*2 + 6*5*2)/(6*5*6*6) = 4/36 = 11,11%

Δεσμευμενες πιθανοτητες :

P(A/Β) = 2/6
P(A/Γ) = 3/6
P(A/Δ) = 4/6

Θεωρημα Ολικης πιθανοτητας

P(A) = P( A^(ΒUΓUΔ) ) = P( (A^B)U(A^Γ)U(A^Δ) ) = P(A^B) + P(A^Γ) + P(A^Δ) ) = P(A/B)*P(B) + P(A/Γ)*P(Γ) + P(A/Δ)*P(Δ) =

(2/6)*(12/36) + (3/6)*(20/36) + (4/6)*(4/36) => P(A) = 100 / 216 = (5/6) * (5/6)*(4/6) = (1-1/6)*(1-1/6)*(1-2/6).

Το μονο πραγμα που προσαπτεις σε αυτην την αποδειξη ειναι το γιατι εξαιρω τις διπλες στηλες οχι διαφορετικων παιχτων αυτες δεν τις εξαιρω καθολου τις υπολογιζω, αλλα τις διπλες στηλες του ιδιου παιχτη !

Και το προσαπτεις αυτο γιατι προφανως θεωρεις πως στη πραγματικοτητα του τζοκερ το πληθος των παιχτων που θα συμπληρωνουν δελτια με ιδιες στηλες ειναι χιλιαδες και εκατομμυρια που εγω παω παρατυπα και τις βγαζω εκτος δειγματικου χωρου !
Ενω εγω θεωρω πως αυτα τα δελτια θα ειναι μηδεν και γιαυτο τις εξαιρω απο τον δειγματικο χωρο !
Γιαυτο λεω οτι δεν διαφωνουμε στα μαθηματικα αλλα διαφωνουμε για το τι συμβαινει στη πραγματικοτητα των παικτων που παιζουν τζοκερ !

Οποιος πιστευει οτι οι παιχτες τζοκερ παιζουν εκ δελτια με ιδιες στηλες σε καθε δελτιο τοτε ασφαλως και οφειλει να διαφωνησει με την εξαιρεση διπλων στηλων του ιδιου παιχτη που κανω στην αποδειξη !

Σε αυτο που γραφεις εδω εσυ θεωρεις οτι καθε παιχτης παιζει ακριβως μια στηλη, γιαυτο ισχυει αυτο που γραφεις ΑΝ οντως στο τζοκερ καθε παιχτης επαιζε μονο μια στηλη.
Στο πραγματικο τζοκερ ομως οι παικτες παιζουν πανω απο μια στηλη ! Το να πεις οτι δεν με ενδιαφερουν οι παιχτες και ποσες στηλες παιζει καθε παιχτης ειναι σαν να λες πως μια πληροφορια για το πειραμα που σου ειναι ορατη να την κανεις επιτηδες αορατη !

Ειναι σα να σου δινει καποιος κατευθειαν τις διακριτες στηλες και να λες οχι δεν θελω να τις ξερω για να βγει ο τυπος υπολογισμου που επιθυμω.

Παμε παρακατω, η P' της διωνυμικης εκφραζει την πιθανοτητα που υπαρχει σε 24 εκ επαναληψεις του πειραματος σου να προκυψουν s επιτυχιες !

Εσυ τωρα πρεπει να εξηγησεις ΓΙΑΤΙ οι s επιτυχιες στο πειραμα σου σημαινουν s διακριτες στηλες μεσα στις παιγμενες ! Επιτυχια στο πειραμα σου ετσι οπως εσυ την ορισες, ειναι μια στηλη απο τις 24 εκ να μην βρισκεται μεσα στις παιγμενες στηλες αφου θα εχει πολλαπλοτητα ki = 0 !

Πως αυτο ειναι ισοδυναμο με τις διακριτες στηλες των m ? Πρεπει να το εξηγησεις γιατι δεν ειναι αυτονοητο.

Οι m στήλες μέσα στη λίστα με παιγμένες, μπορεί να επαναλαμβάνονται, αλλά εξακολουθεί να υπάρχει το ενδεχόμενο κάποια στήλη από τις ν=24435180 να έχει παραλειφθεί από τις παιγμένες. Και δεν εννοώ να έχει παραλειφθεί μόνο μία στήλη από τις ν, αλλά μία ή περισσότερες από τις ν. Αυτό περιορίζει τον αριθμό των διακριτών στηλών μέσα στις παιγμένες από ν σε s. Οι παιγμένες είναι m και μέσα τους υπάρχουν s διακριτές, όπου s≤v.

Έβαλα k_i=0 αν έχει παραλειφθεί η στήλη i από τις v. Μια υπο-ομάδα των k_i (i=1..ν) θα έχει πλήθος s, άθροισμα m, ενώ τα υπόλοιπα θα είναι μηδενικά. Ε το κόλπο ο κόπος είναι πώς υπεισέρχονται (v-s) μηδενικά σε v προσθετέους του αθροίσματος m.

Ε δεν ξέρω τι άλλο να πω 10 χρονών ανίψι έχω θα το καταλάβει.

Οχι δεν θα το καταλαβει ετσι οπως το λες !

Τοσην ωρα σου ζηταω να μου υποδειξεις ποια ειναι η εξισωση που σου προσφερει η διωνυμικη και σε αυτην την εξισωση που ειναι ο αγνωστος διακριτες στηλες που θα υπολογισεις και ποιοι ειναι οι γνωστοι και δεν μου δειχνεις ουτε την εξισωση ουτε ουτε τον αγνωστο !

Παμε παλι η διωνυμικη σου δινει μια εξισωση P' = F(ν,s,m)

Σε αυτην την εξισωση ποιοι ειναι οι γνωστοι και ποιοι οι αγνωστοι που υπολογιζεις ! Για να βρω το s σε αυτην την εξισωση ΠΡΕΠΕΙ να γνωριζω το P' το οποιο για να το υπολογισεις πρεπει να ξερεις το s που εσυ ψαχνεις !

Αν καποιος σου δωσει το P', ηδη γνωριζεις το ν και το m, αρα με καποια επαναληπτικη διαδικασια λυνεις την εξισωση και υπολογιζεις το s το οποιο θα ειναι οι φορες που στις ν = 24 εκ δοκιμες ΔΕΝ ηρθαν στηλες που βρισκονται στις παιγμενες με πιθανοτητα P' ! Αυτο που μολις εγραψα σημαινει πως το s ΔΕΝ ΕΙΝΑΙ οι διακριτες στηλες των παιγμενων ετσι οπως πηγες και ορισες την επιτυχια στο πειραμα σου ! Το s ειναι οι διακριτες στηλες αυτων που ΔΕΝ παιχτηκαν και γιαυτο δεν εμφανιστηκαν στις παιγμενες εχοντας ki=0 ! Αρα για να βρεις τις διακριτες στηλες των παιγμενων m πρεπει να αφαιρεσεις απτα 24 εκ το s !

Τοσην ωρα προσπαθω να σου δειξω πως ετσι οπως πηγες και ορισες την επιτυχια στο πειραμα σου το s ΔΕΝ ΕΙΝΑΙ οι διακριτες στηλες των παιγμενων, κι ο αντιλογος ειναι οτι μικρα παιδια θα σε καταλαβαιναν ... αμα δε βγαλεις και το τουπε δεν μπορεις ...


Με λιγα λογια επρεπε να ορισεις σαν επιτυχια στο πειραμα σου το αναποδο δηλ. ki>0 !!! αλλάζοντας αντιστοιχα και τον τυπο p που ετσι κι αλλιως τον μεταφερεις χωρις να τον καταλαβαινεις γιατι ειναι ετσι ! ΤΟΤΕ πραγματι το s ΘΑ ΗΤΑΝ οι διακριτες στηλες των παιγμενων !

Και πολυ ωραια τα διορθωνεις τα παραπανω, αλλα το P' απο που στο διαολο το βρισκεις ωστε στην P' = F(ν,s,m), ο μοναδικος αγνωστος να ειναι το s ?

Μην μου πεις απο την διωνυμικη γιατι η διωνυμικη ειναι η εξισωση που λυνεις !

Για να εχεις την απαιτηση να καταλαβει κατι ακομα και παιδακι, ΠΡΕΠΕΙ ΝΑ ΤΟ ΕΧΕΙΣ πρωτα καταλαβει εσυ ! Το εχεις ?

[Ανίκητος]

Στο απεδειξα αυτο που ζητας οταν ν=6 (μια ζαρια) και παιχτες = 3 ! Μπορεις να πας εκει και να μου αποδειξεις το λαθος ! Και μην μου πεις για παιδικα υπαρχει κατι που λεγεται και αναδρομικη αποδειξη. (αποδειξη για ν-1, για ν=ν, για ν=ν+1), δεν χρειαζεται να παιδευεσαι με τα εκ συνδυασμων ντε και καλα.

SpoilerShow

Ορισμοι :

U = ενωση (ή)
/ = δεσμευμενη πιθανοτητα
^ = τομη (και)

Ενδεχομενο να μην πετυχει κανενας το αποτελεσμα της ζαριας = Α
Ενδεχομενο να ειναι και τα 4 πονταρισματα διαφορετικα = Β
Ενδεχομενο να ειναι ιδια μονο 2 πονταρισματα = Γ = 3 διαφορετικα πονταρισματα
Ενδεχομενο να ειναι ιδια μονο 3 πονταρισματα = Δ = 2 διαφορετικα πονταρισματα

Λύση :

Απο τη στιγμη που ο ενας απο τους τρεις πχωρουμιτες θα παιξει 2 διαφορετικα πονταρισματα και οχι ΙΔΙΑ, δεν προκειται να εμφανιστουν ΠΟΤΕ 4 ιδια πονταρισματα, οποτε ολοι οι δυνατοι συνδυασμοι των 4 πονταρισματων ΔΕΝ θα ειναι 6*6*6*6, αλλα θα ειναι (6*5)*6*6 !

Τα Β,Γ,Δ και παλι ειναι ξενα μεταξυ τους και η ενωση τους εχει πιθανοτητα 1 ! Και συγκεκριμενα :

P(Β) = (6*5*4*3)/(6*5*6*6) = 12/36 = 33.33%
P(Γ) = (6*5 *4 + 2*6*4*5 +2*6*4*5) /(6*5*6*6) = 20/36 = 55,55%
P(Δ) = (6*5*2 + 6*5*2)/(6*5*6*6) = 4/36 = 11,11%

Δεσμευμενες πιθανοτητες :

P(A/Β) = 2/6
P(A/Γ) = 3/6
P(A/Δ) = 4/6

Θεωρημα Ολικης πιθανοτητας

P(A) = P( A^(ΒUΓUΔ) ) = P( (A^B)U(A^Γ)U(A^Δ) ) = P(A^B) + P(A^Γ) + P(A^Δ) ) = P(A/B)*P(B) + P(A/Γ)*P(Γ) + P(A/Δ)*P(Δ) =

(2/6)*(12/36) + (3/6)*(20/36) + (4/6)*(4/36) => P(A) = 100 / 216 = (5/6) * (5/6)*(4/6) = (1-1/6)*(1-1/6)*(1-2/6).

Καταρχήν στο spoiler έχεις παραλείψει γραμμές, για να μην δείξεις τις υποθέσεις για τα πονταρίσματα στο ζάρι, αλλά μόνο τους ορισμούς των ενδεχομένων. Προτείνω να διορθώσεις τουλάχιστον το λάθος στην επικόλληση.

Προσκόμισε και την αναδρομική απόδειξη λοιπόν, για να ολοκληρωθεί ότι αυτό που λες, εφόσον ισχύει στο ζάρι, θα πρέπει να ισχύει και στο τζόκερ. Με μισές δουλειές και μισές επικολλήσεις, δεν αποδεικνύεται κανένας ισχυρισμός.

Ούτως ή άλλως δεν σου ζήτησα ντε και καλά απόδειξη, αλλά να μου εξηγήσεις ποιο από τα δύο ισχύει:
P(Α_i|A_j)<P(Α_i) ή P(Α_i|A_j)>P(Α_i).

Το αντίστοιχο πράγμα δηλαδή, των δεσμευμένων πιθανοτήτων που παρουσιάζεις στην μαθηματική απόδειξη ως θέσφατες.

Το μονο πραγμα που προσπαπτεις σε αυτην την αποδειξη ειναι γιατι εξαιρω τις διπλες στηλες οχι διαφορετικων παιχτων αυτες δεν τις εξαιρω, αλλα του ιδιου παιχτη ! Και το προσαπτεις αυτο γιατι προφανως θεωρεις πως στη πραγματικοτητα του τζοκερ το πληθος των παιχτων που θα συμπληρωνουν δελτια με ιδιες στηλες ειναι χιλιαδες και εκατομμυρια ενω εγω θεωρω πως θα ειναι μηδεν ! Γιαυτο λεω που δεν διαφωνουμε στα μαθηματικα διαφωνουμε για το τι συμβαινει στη πραγματικοτητα των παικτων που παιζουν τζοκερ !

Αυτό που σου έχω προσάψει είναι η κατασκευή ενός διαφορετικού δειγματικού χώρου από αυτόν που ισχύει όταν μεταχειρίζεσαι την πληροφορία που υποθέτεις ότι δεν πρέπει να μεταχειριστείς.

Σε αυτο που γραφεις εδω εσυ θεωρεις οτι καθε παιχτης παιζει ακριβως μια στηλη, γιαυτο ισχυει αυτο που γραφεις. Το να πεις οτι δεν με ενδιαφερουν οι παιχτες ειναι σαν μια πληροφορια για το πειραμα που σου ειναι ορατη να την κανεις επιτηδες αορατη ! Ειναι σα να σου δινει καποιος κατευθειαν τις διακριτες στηλες και να λες οχι δεν θελω να τις ξερω για να βγει ο τυπος υπολογισμου που επιθυμω.

Για άλλη μια φορά: Δεν ξέρω πόσοι παίκτες παίζουν πόσες στήλες, δεν με απασχολεί, πέρα από τι στήλες παίζουν συγκεντρωτικά.

Ποια πληροφορία είναι ορατή για τους παίκτες; Τα στερεότυπα που έχουμε εσύ και εγώ, με τα οποία διαφωνούμε; Έχεις συναντήσει κάθε Αθηναίο και κάθε Θεσσαλονικιό και κάθε Έλληνα ή ξένο παίκτη τζόκερ για να γνωρίζεις καλύτερα από όλους ποιες στήλες παίζουν;

Εγώ έχω δει τουλάχιστον έναν παίκτη να παίζει δυο φορές την ίδια στήλη σε μία κλήρωση τζόκερ. Μου κάνει ορατή την πληροφορία ότι γίνεται ένας παίκτης να παίξει τις ίδιες στήλες, για την οποία συμφωνούμε πως είναι άχρηστη, για τους δικούς του λόγους ο καθένας. Εμένα επειδή δεν μ' απασχολεί, εσύ επειδή πιστεύεις ότι οι παίκτες δεν το κάνουν στην πράξη.

Πιθανότητα να υπάρχει νικητής σε μια κλήρωση τζόκερ, προκύπτει από το πλήθος των διακριτών στηλών στη συγκεντρωτική λίστα των παιγμένων στηλών. Πιθανότητα να υπάρχει νικητής, μπορεί επίσης να προκύπτει και από το ποιος παίκτης παίζει τι, αλλά μπες εσύ στη διαδικασία. Εγώ μπήκα στη δική μου διαδικασία και ανακάλυψα και προσκόμισα, να τα δείτε.

Τοσην ωρα σου ζηταω να μου υποδειξεις ποια ειναι η εξισωση που σου προσφερει η διωνυμικη και σε αυτην την εξισωση που ειναι ο αγνωστος διακριτες στηλες που θα υπολογισεις και δεν μου δειχνεις ουτε την εξισωση ουτε ουτε τον αγνωστο !

Παμε αλι η διωνυμικη σου δινει μια εξισωση P' = F(ν,s,m)

Σε αυτην την εξισωση ποιοι ειναι οι γνωστοι και ποιοι οι αγνωστοι που υπολογιζεις ! Για να βρω το s σε αυτην την εξισωση ΠΡΕΠΕΙ να γνωριζω το P' το οποιο για να το υπολογισεις πρεπει να ξερεις το s που εσυ ψαχνεις !

Αν καποιος σου δωσει το P' γνωριζεις το ν και το m, αρα με καποια επαναληπτικη διαδικασια λυνεις την εξισωση και υπολογιζεις το s το οποιο θα ειναι οι φορες που στις ν = 24 εκ δοκιμες ΔΕΝ ηρθαν στηλες που βρισκονται στις παιγμενες με πιθανοτητα P' ! Πολυ ωραια το P' απο που το βρισκεις ?

Μην μου πεις απο την διωνυμικη γιατι η διωνυμικη ειναι η εξισωση που λυνεις !

Δεν μου προσφέρει κάποια εξίσωση η διωνυμική, μου προσφέρει έναν τύπο να υπολογίζω την πιθανότητα του πλήθους των διακριτών στηλών μέσα στις m παιγμένες στήλες μιας κλήρωσης να είναι s.

Prob{ο αριθμός διακριτών στηλών της λίστας των παιγμένων είναι ακριβώς s} = f(s,v,p) = C(v,s)*(m/m+v-1)^s * (v-1/m+v-1)^(v-s)

https://en.wikipedia.org/wiki/Binomial_ ... efinitions

Το m που υπεισέρχεται στον τύπο το βρίσκω από τον διοργανωτή του τζόκερ, διαφέρει από κλήρωση σε κλήρωση.