Τα τυχερά παιχνίδια είναι στημένα

[nik_killthemall]

Ο 1ος έχει πιθανότητα 5/6 να μην πετύχει το αποτέλεσμα της ζαριάς. Το ίδιο κι ο δεύτερος. Το ίδιο κι ο τρίτος. Άρα (5/6)^3.

Θες πιο αναλυτικά;

Ρε μαν αυτο αποδεικνυω με μαθηματικα στην αποδειξη, διαβασε τη λιγο και θα γινουν ολα ξεκαθαρα !

Την πιθανοτητα 5/6 που γραφεις την εχουν ΜΕ ΤΟΝ ΟΡΟ ο παρατηρητης που τους την αποδιδει να μην μαθει ποτε το πονταρισμα τους ! Μονο τοτε τα ενδεχομενα αποτυχιας του καθε πονταρισματος ειναι ανεξαρτητα και αυτη η ανεξαρτησια σου επιτρεπει να πολλαπλασιαζεις τις πιθανοτητες !

Αν ο παρατηρης ομως μαθει τα πονταρισματα, αυτο που γραφεις δεν ισχυει, και τα ενδεχομενα αποτυχιας καθε πονταρισματος παυουν να ειναι ανεξαρτητα.

Οπως γραφω και στην αποδειξη συμβαινουν ΔΥΟ πειραματα, η υπερθεση των οποιων δινει αυτο που γραφεις, αν το αποτελεσμα του πρωτου πειραματος ειναι γνωστο, τοτε αυτο που γραφεις δεν ισχυει.

ΩΣΤΟΣΟ το αδυνατο σημειο ακομα κι οταν ο παρατηρητης δεν μαθει το πονταρισμα τους, ειναι οτι εκεινη η στηλη που γραφεις ¨ποσες φορες παιχτηκε η στηλη" στον υπολογισμο σας θεωρειται ΙΣΟΠΙΘΑΝΗ !
Δηλ. στον υπολογισμο σας θεωρειτε ιδια πιθανοτητα να εμφανιστει συνδυασμος 4.999.999 ιδιων στηλων με το να εμφανιστει συνδυασμος 10 ιδιων στηλων. Και οτι το θεωρειτε αυτο στον υπολογισμο το βλεπεις κατα τη διαρκεια της αποδειξης που οδηγει στον μαθηματικο τυπο σας (αλλου δεν φαινεται και οσες φορες ρωτησα τους προφεσορους δεν ξεραν τη τυφλα τους) !

Αυτη η παραδοχη ομως ιδιας πιθανοτητας σε ολους τους συνδυασμους στηλων δεν ισχυει ! Δεν εχουν ολοι οι συνδυασμοι στηλων την ιδια πιθανοτητα !

[Ανίκητος]

ΩΣΤΟΣΟ το αδυνατο σημειο ακομα κι οταν ο παρατηρητης δεν μαθει το πονταρισμα τους, ειναι οτι εκεινη η στηλη που γραφεις ¨ποσες φορες παιχτηκε η στηλη" στον υπολογισμο σας θεωρειται ΙΣΟΠΙΘΑΝΗ !
Δηλ. στον υπολογισμο σας θεωρειτε ιδια πιθανοτητα να εμφανιστει συνδυασμος 4.999.999 ιδιων στηλων με το να εμφανιστει συνδυασμος 10 ιδιων στηλων. Και οτι το θεωρειτε αυτο στον υπολογισμο το βλεπεις κατα τη διαρκεια της αποδειξης που οδηγει στον μαθηματικο τυπο σας (αλλου δεν φαινεται και οσες φορες ρωτησα τους προφεσορους δεν ξεραν τη τυφλα τους) !

Αυτη η παραδοχη ομως ιδιας πιθανοτητας σε ολους τους συνδυασμους στηλων δεν ισχυει ! Δεν εχουν ολοι οι συνδυασμοι στηλων την ιδια πιθανοτητα !

Δεν μπορώ να σε παρακολουθήσω εύκολα.
Κάθε στήλη έχει πιθανότητα p να ταιριάζει με αυτή που θα βγάλει η κληρωτίδα, ασχέτως εάν δεν παίχτηκε (μηδέν, 0) από τους παίκτες, ή παίχτηκε μία ή περισσότερες φορές από αυτούς.
Ζήτησες την πιθανότητα να βρεθεί νικήτρια στήλη σε αυτές που παίχτηκαν, με συγκεκριμένη συμμετοχή που ακολούθησε το ενδεχόμενο Α, δηλαδή 48 εκ. παιγμένες στήλες, εκ των οποίων οι 21 εκ. μοναδικές και διαφορετικές μεταξύ τους, που σημαίνει ότι παίχθηκαν ακριβώς 1 φορά.

Όταν μιλάς για "συνδυασμό 10 ίδιων στηλών", εγώ καταλαβαίνω "επαναλήψεις", ότι κάποιο κελί στον πρώτο πίνακα (κάτω από D) έχει τον αριθμό 10 και ταυτόχρονα 10 γραμμές στον δεύτερο πίνακα έχουν τον ίδιο αύξοντα αριθμό "σειράς" (δηλαδή θα επιλέξεις 10 κελιά κάτω από το F για να συμπληρώσεις στο αντίστοιχο κελί κάτω από το G, τον ίδιο αριθμό σειράς από το σύνολο {1,...,24435180}). Καταλαβαίνω καλά;



Οπότε με αυτή την αναπαράσταση των δυο πινάκων μπορείς να καταλάβεις ότι είναι ισοπίθανα τα ενδεχόμενα ανάμεσα στις στήλες του τζόκερ να ταιριάξουν με την κληρωμένη, ενώ η πιθανότητα ανάμεσα στις στήλες που παίχτηκαν να ταιριάζουν με την κληρωμένη είναι ανάλογη των επαναλήψεών τους, αν υπάρχουν.

Τι ψάχνεις;

[Ανίκητος]

Οι πιθανότητες επιτυχίας με 5 νούμερα και όλα τα τζοκερ είναι οι μεγαλύτερες.

5 νούμερα με όλα τα Τζόκερ είναι 20 στήλες.

Αν παίξω 20 απλά δελτία με ένα τζόκερ και 5 νούμερα, οι πιθανότητες για 5+1 είναι ίδιες.

Καλω τον hellegennes να τοποθετηθεί επ αυτου.

Εγώ λέω ότι μια 5αδα με όλα τα τζοκερ μου δίνει περισσότερες πιθανότητες να κερδίσω, ο mao mao λέει ότι αν παίξει 20 διαφορετικές 5αδες με ένα τζοκερ έχει τις ίδιες πιθανότητες με μένα.

Αυτόν τον πίνακα ήθελα να βρω:


Αν έχεις παίξει 20 στήλες και πιάσεις το τζόκερ, η πιθανότητα να βρεθείς σε κατηγορία που κερδίζει είναι 3,71 φορές μεγαλύτερες από ό,τι να έχεις παίξει 20 στήλες και να μην πιάσεις το τζόκερ.

[Στύξ]

Κάτι σαν τη λαχειοφόρο της ΑΑΔΕ, που κερδίζει ο κανένας.

[nik_killthemall]

ΩΣΤΟΣΟ το αδυνατο σημειο ακομα κι οταν ο παρατηρητης δεν μαθει το πονταρισμα τους, ειναι οτι εκεινη η στηλη που γραφεις ¨ποσες φορες παιχτηκε η στηλη" στον υπολογισμο σας θεωρειται ΙΣΟΠΙΘΑΝΗ !
Δηλ. στον υπολογισμο σας θεωρειτε ιδια πιθανοτητα να εμφανιστει συνδυασμος 4.999.999 ιδιων στηλων με το να εμφανιστει συνδυασμος 10 ιδιων στηλων. Και οτι το θεωρειτε αυτο στον υπολογισμο το βλεπεις κατα τη διαρκεια της αποδειξης που οδηγει στον μαθηματικο τυπο σας (αλλου δεν φαινεται και οσες φορες ρωτησα τους προφεσορους δεν ξεραν τη τυφλα τους) !

Αυτη η παραδοχη ομως ιδιας πιθανοτητας σε ολους τους συνδυασμους στηλων δεν ισχυει ! Δεν εχουν ολοι οι συνδυασμοι στηλων την ιδια πιθανοτητα !

Δεν μπορώ να σε παρακολουθήσω εύκολα.

Μαν εδώ βλέπεις την ΜΑΘΗΜΑΤΙΚΗ ΑΠΟΔΕΙΞΗ του τυπου που υποστηρίζετε για το αναλογο με τη ζαρια και τους 3 πχωρουμιτες που εθεσε ο μαο μαο.

SpoilerShow

Ορισμοι :

U = ενωση (ή)
/ = δεσμευμενη πιθανοτητα
^ = τομη (και)

Ενδεχομενο να μην πετυχει κανενας το αποτελεσμα της ζαριας = Α
Ενδεχομενο να ειναι και τα 3 πονταρισματα διαφορετικα = Β
Ενδεχομενο να ειναι ιδια μονο 2 πονταρισματα = Γ
Ενδεχομενο να ειναι ιδια και τα 3 πονταρισματα = Δ

Λύση :

Τα Β,Γ,Δ ειναι ξενα μεταξυ τους και η ενωση τους εχει πιθανοτητα 1 !

P(Β) = (6*5*4)/(6*6*6) = 20/36 = 55.55%
P(Γ) = 3*(6*5)/(6*6*6) = 15/36 = 41,66%
P(Δ) = (6)/(6*6*6) = 1/36 = 2,77%

Δεσμευμενες πιθανοτητες :

P(A/Β) = 3/6
P(A/Γ) = 4/6
P(A/Δ) = 5/6

Θεωρημα Ολικης πιθανοτητας

P(A) = P( A^(ΒUΓUΔ) ) = P( (A^B)U(A^Γ)U(A^Δ) ) = P(A^B) + P(A^Γ) + P(A^Δ) ) = P(A/B)*P(B) + P(A/Γ)*P(Γ) + P(A/Δ)*P(Δ) =

(3/6)*(20/36) + (4/6)*(15/36) + (5/6)*(1/36) => P(A) = 125 / 216= (1-1/6)^3.

Εκει που εχω μπολνταρει, βλεπεις τον υπολογισμο της πιθανοτητας οι πχωρουμιτες να κανουν ιδια πονταρισματα ή διαφορετικα ! Οπως βλεπεις ολοι οι συνδυασμοι πονταρισματων των πχωρουμιτων ειναι 6*6*6 = 216 και θεωρουνται ολοι ΙΣΟΠΙΘΑΝΟΙ !

Γιαυτον το λογο στον υπολογισμο πιθανοτητας στο μπολντ που βλεπεις χρησιμοποιειται ο τυπος = ευνοικες περιπτωσεις / συνολικες δυνατες περιπτωσεις. Αυτος ο τυπος χρησιμοποιειται ΜΟΝΟ για ισοπιθανα ενδεχομενα, και εδω ειναι πραγματι ισοπιθανα γιατι το πονταρισμα των πχωρουμιτων ειναι ενας μονο αριθμος ! Ισοπιθανα σημαινει πως η πιθανοτητες τα πονταρισματα των πχωρουμιτων να ειναι π.χ. (1,1,1) ή (1,2,3) ειναι ακριβως ΙΔΙΕΣ και ισες με 1/216 η καθε μια !
Οποτε με αυτη τη προϋποθεση ΙΣΟΠΙΘΑΝΩΝ ΣΥΝΔΥΑΣΜΩΝ προκύπτει ο τυπος που χρησιμοποιειτε για τον υπολογισμο πιθανοτητας νικητη ! Χωρις την παραδοχη αυτη - πως ολοι οι συνδυασμοι πονταρισματων ειναι ισοπιθανοι - ο τυπος που χρησιμοποιειτε παει στα σκουπιδια !

_____________

Στη περιπτωση ΤΩΡΑ του τζοκερ, το πονταρισμα ειναι η στηλη η οποια αποτελειται ΟΧΙ απο εναν αριθμο αλλα απο 5 + 1 αριθμους ! Και η επιλογη αυτων των 5+1 αριθμων για καθε συμμετασχοντα παιχτη ΔΕΝ γινεται τυχαια απο μια κληρωτιδα, αλλα την φτιαχνει Ο ΙΔΙΟΣ ο παιχτης ! Επειδη λοιπον τη φτιαχνει ο ιδιος ο παιχτης, προσπαθωντας να μιμηθει την τυχη, εξαιρει ΑΥΤΟΜΑΤΑ όλες τις 5αδες που εχουν οποιοδηποτε μαθηματικο ή γεωμετρικο πατερν !

Αυτο σημαινει πως σε 5 εκ παιγμενες στηλες ΔΕΝ ΘΑ ΕΜΦΑΝΙΣΤΟΥΝ ΠΟΤΕ 100 ιδιες ή 1000 ιδιες ή 1 εκ ιδιες στηλες με αριθμους :

1,2,3,4,5 + τζοκερ 6 ή
2,4,6,8,10 + τζοκερ 12 ή
3,6,9,12,15 + τζοκερ 18
κοκ

Ακομα κι αν καποιος παιξει μια δυο τετοιου τυπου στηλες ΔΕΝ θα δεις ποτε αυτες τις στηλες να επαναλαμβανονται 100 ή 150 ή 1000, ή 2 εκ φορες μεσα στις 5 εκ παιγμενες στηλες ! ΠΟΤΕ !

Ωστοσο ο τυπος που χρησιμοποιειτε εσεις θεωρει πως ολες αυτες οι επαναλαμβανομενες στηλες θα εμφανιστουν 100, 150, 1000, 1εκ κλπ φορες μεσα στα 5 εκ παιγμενων στηλων ΜΕ ΤΗΝ ΙΔΙΑ ΑΚΡΙΒΩΣ πιθανοτητα που θα εμφανιστουν και ολοι οι υπολοιποι συνδυασμοι !

Αυτην την αστοχια, ερχονται στη πραγματικοτητα και την λυνουν οι κατανομες πιθανοτητων που ειναι ανομοιομορφες και ΑΠΑΓΟΡΕΥΟΥΝ στους συνδυασμους να ειναι ισοπιθανοι ! Δηλ. μεγενθυνουν την πιθανοτητα σε μια περιοχη συνδυασμων και εξαφανιζουν την πιθανοτητα απο μια αλλη περιοχη συνδυασμων ! Με λιγα οι κατανομες πιθανοτητων πανε και ΥΠΟΘΕΤΟΥΝ ΕΥΣΤΟΧΑ ποσες ειναι διπλες τριπλες κλπ στηλες στα 5εκ παιγμενων στηλων !

[Ανίκητος]

Εκει που εχω μπολνταρει, βλεπεις τον υπολογισμο της πιθανοτητας οι πχωρουμιτες να κανουν ιδια πονταρισματα ή διαφορετικα ! Οπως βλεπεις ολοι οι συνδυασμοι πονταρισματων των πχωρουμιτων ειναι 6*6*6 = 216 και θεωρουνται ολοι ΙΣΟΠΙΘΑΝΟΙ !

Γιαυτον το λογο στον υπολογισμο πιθανοτητας στο μπολντ που βλεπεις χρησιμοποιειται ο τυπος = ευνοικες περιπτωσεις / συνολικες δυνατες περιπτωσεις. Αυτος ο τυπος χρησιμοποιειται ΜΟΝΟ για ισοπιθανα ενδεχομενα, και εδω ειναι πραγματι ισοπιθανα γιατι το πονταρισμα των πχωρουμιτων ειναι ενας μονο αριθμος ! Ισοπιθανα σημαινει πως η πιθανοτητες τα πονταρισματα των πχωρουμιτων να ειναι π.χ. (1,1,1) ή (1,2,3) ειναι ακριβως ΙΔΙΕΣ και ισες με 1/216 η καθε μια !
Οποτε με αυτη τη προϋποθεση ΙΣΟΠΙΘΑΝΩΝ ΣΥΝΔΥΑΣΜΩΝ προκύπτει ο τυπος που χρησιμοποιειτε για τον υπολογισμο πιθανοτητας νικητη ! Χωρις την παραδοχη αυτη - πως ολοι οι συνδυασμοι πονταρισματων ειναι ισοπιθανοι - ο τυπος που χρησιμοποιειτε παει στα σκουπιδια !

Η συνήθης παραδοχή που γίνεται είναι ότι τα απλά ενδεχόμενα είναι μεταξύ τους ισοπίθανα. Ο "συνδυασμός πονταρισμάτων" όπως το (1,1,1) είναι μία περίπτωση στις συνολικές δυνατές περιπτώσεις, άρα απλό ενδεχόμενο. Το (1,2,3) είναι κι αυτό μια περίπτωση στις συνολικές δυνατές, για αυτό υπάρχει ο όρος απλό ενδεχόμενο. Στο λύκειο που οι περιπτώσεις είναι πεπερασμένου αριθμού, μαζεύουμε όλα τα απλά ενδεχόμενα στο σύνολο Ω. Αν δεν έχουμε κάποιο λόγο να αποδώσουμε άνισες πιθανότητες, κατανέμουμε την ίδια πιθανότητα.

Στη περιπτωση ΤΩΡΑ του τζοκερ, το πονταρισμα ειναι η στηλη η οποια αποτελειται ΟΧΙ απο εναν αριθμο αλλα απο 5 + 1 αριθμους ! Και η επιλογη αυτων των 5+1 αριθμων για καθε συμμετασχοντα παιχτη ΔΕΝ γινεται τυχαια απο μια κληρωτιδα, αλλα την φτιαχνει Ο ΙΔΙΟΣ ο παιχτης ! Επειδη λοιπον τη φτιαχνει ο ιδιος ο παιχτης, προσπαθωντας να μιμηθει την τυχη, εξαιρει ΑΥΤΟΜΑΤΑ όλες τις 5αδες που εχουν οποιοδηποτε μαθηματικο ή γεωμετρικο πατερν !

Εδώ ξεφεύγουμε από τις πιθανότητες. Αυτό είναι μια θεωρία συμπεριφοράς για το πώς νομίζεις ότι παίζουν οι παίκτες. Αν η βάση της θεωρίας είναι να "μιμηθούν την τύχη" αποφεύγοντας αυτά που εκείνοι αναγνωρίζουν για "πάτερν", αφενός διαφωνώ, για το τι αντιλαμβάνονται ως "τυχαίο" και τι όχι. Αφετέρου θα θυμηθώ παλιές μου αναμνήσεις που έπαιζα και υπήρχαν έτοιμα να αγοράσεις, συμπληρωμένα δελτία εκτυπωμένα από μηχανή, ακριβώς με στήλες "γεωμετρικά φτιαγμένες" σαν κι αυτές που ισχυρίζεσαι πως αποφεύγουν:

Αυτο σημαινει πως σε 5 εκ παιγμενες στηλες ΔΕΝ ΘΑ ΕΜΦΑΝΙΣΤΟΥΝ ΠΟΤΕ 100 ιδιες ή 1000 ιδιες ή 1 εκ ιδιες στηλες με αριθμους :

1,2,3,4,5 + τζοκερ 6 ή
2,4,6,8,10 + τζοκερ 12 ή
3,6,9,12,15 + τζοκερ 18
κοκ

Ακομα κι αν καποιος παιξει μια δυο τετοιου τυπου στηλες ΔΕΝ θα δεις ποτε αυτες τις στηλες να επαναλαμβανονται 100 ή 150 ή 1000, ή 2 εκ φορες μεσα στις 5 εκ παιγμενες στηλες ! ΠΟΤΕ !

Εγώ νομίζω ότι θα βρεις πολλούς να παίζουν γνώριμα αριθμητικά ή γεωμετρικά μοτίβα από τη ζωή τους, π.χ. το τηλέφωνό τους, την ημερομηνία γέννησης, ή να σχεδιάζουν γραμμές και καρδούλες με τη διάταξη των αριθμών πάνω στο χάρτινο δελτίο. Κάθε παίκτης έχει διαφορετικές αντιλήψεις για προτιμητέες και αποφευκτέες στήλες. Επιπλέον, σε αυτό που θα προτιμήσει ή θα αποφύγει ο ένας παίκτης, ο άλλος παίκτης θα κάνει το ανάποδο, δηλαδή το ποντάρισμα ανακατεύεται.

Το αποτέλεσμα της κληρωτίδας είναι αυτό που θα πρέπει να μαντέψουν οι παίκτες. Η κληρωτίδα όμως δεν έχει προτιμήσεις οπότε ένα αποτέλεσμα όπως το 1,2,3,4,5 + τζόκερ 6 είναι εξίσου πιθανό όσο κάθε άλλο μέσα στα 24.435.180 δυνατά αποτελέσματα. (Ώσπου ένας κορυφαίος φυσικός μας δείξει πώς η κλήρωση γίνεται πιο προβλέψιμη, αν και μάλλον θα λαμβάνει υπόψη ακόμη και το 3ο δεκαδικό ψηφίο από τον πυρετό αυτουνού που πατάει το κουμπί για την έναρξη της κλήρωσης ).

Κι αφού η κληρωτίδα δεν έχει προτιμήσεις, οι παίκτες πιέζονται να προσαρμοστούν σε αυτό και να κάνουν πιο ανοιχτόμυαλα τις επιλογές τους σε στήλες, παρά να τις βρίσκουν γρουσούζες.

Και εν τέλει, πόσες πια είναι αυτές οι στήλες τζόκερ που ισχυρίζεσαι ότι όλοι οι παίκτες αποφεύγουν να παίξουν; Εκατό χιλιάδες; Πεντακόσιες χιλιάδες; Με ποιο σκεπτικό είναι στατιστικά σημαντικό;

Ωστοσο ο τυπος που χρησιμοποιειτε εσεις θεωρει πως ολες αυτες οι επαναλαμβανομενες στηλες θα εμφανιστουν 100, 150, 1000, 1εκ κλπ φορες μεσα στα 5 εκ παιγμενων στηλων ΜΕ ΤΗΝ ΙΔΙΑ ΑΚΡΙΒΩΣ πιθανοτητα που θα εμφανιστουν και ολοι οι υπολοιποι συνδυασμοι !

Αυτην την αστοχια, ερχονται στη πραγματικοτητα και την λυνουν οι κατανομες πιθανοτητων που ειναι ανομοιομορφες και ΑΠΑΓΟΡΕΥΟΥΝ στους συνδυασμους να ειναι ισοπιθανοι ! Δηλ. μεγενθυνουν την πιθανοτητα σε μια περιοχη συνδυασμων και εξαφανιζουν την πιθανοτητα απο μια αλλη περιοχη συνδυασμων ! Με λιγα οι κατανομες πιθανοτητων πανε και ΥΠΟΘΕΤΟΥΝ ΕΥΣΤΟΧΑ ποσες ειναι διπλες τριπλες κλπ στηλες στα 5εκ παιγμενων στηλων !

Όχι, με κάποια άλλη κατανομή πιθανοτήτων δεν ξεπερνάς την αστοχία. Δεν έχεις καν μια εξήγηση για το ποιες "περιοχές συνδυασμών" πρέπει να αποκτήσουν καλύτερες πιθανότητες από τις άλλες, προκειμένου να επιλέξεις μια "κατανομή πιθανοτήτων" (που οι καθιερωμένες κάνουν μετατροπές της ομοιόμορφης κατανομής, πηγαίνοντας από την μια τυχαία μεταβλητή στην άλλη). Εξήγηση πάντως δεν είναι να μου φέρεις μια υποκειμενική αντίληψη για τη συμπεριφορά ενός συνόλου παικτών.

Σε τέτοιες περιπτώσεις παίρνεις τα εμπειρικά δεδομένα του παρελθόντος, συγκεντρώνεις δηλαδή τις κατά μέσο όρο 3-4 εκατομμύρια στήλες ανά παιχνίδι, που έχουν παιχθεί από τους παίκτες στο παρελθόν, για να αναλύσεις στατιστικά αν υπάρχουν σημαντικές μεροληψίες υπέρ κάποιων στηλών, για να βρεις ποιες προτιμάει και ποιες αποφεύγει να παίζει... και μετά; Μετά θα σχηματίσεις ένα κατά πολύ βελτιωμένο ενδεχόμενο του Α, που έχει ακριβέστερη τη συχνότητα των 24.435.180 δυνατών επιλογών; Και τι θα κάνεις με αυτό, θα υπολογίσεις καλύτερη πιθανότητα να βρεθεί νικητής, σύμφωνα με τη θεωρία σου για τη συμπεριφορά των παικτών τζόκερ;

Θέλω να σε δω να τραβάς τέτοια ζόρια.

[nik_killthemall]

Εκει που εχω μπολνταρει, βλεπεις τον υπολογισμο της πιθανοτητας οι πχωρουμιτες να κανουν ιδια πονταρισματα ή διαφορετικα ! Οπως βλεπεις ολοι οι συνδυασμοι πονταρισματων των πχωρουμιτων ειναι 6*6*6 = 216 και θεωρουνται ολοι ΙΣΟΠΙΘΑΝΟΙ !

Γιαυτον το λογο στον υπολογισμο πιθανοτητας στο μπολντ που βλεπεις χρησιμοποιειται ο τυπος = ευνοικες περιπτωσεις / συνολικες δυνατες περιπτωσεις. Αυτος ο τυπος χρησιμοποιειται ΜΟΝΟ για ισοπιθανα ενδεχομενα, και εδω ειναι πραγματι ισοπιθανα γιατι το πονταρισμα των πχωρουμιτων ειναι ενας μονο αριθμος ! Ισοπιθανα σημαινει πως η πιθανοτητες τα πονταρισματα των πχωρουμιτων να ειναι π.χ. (1,1,1) ή (1,2,3) ειναι ακριβως ΙΔΙΕΣ και ισες με 1/216 η καθε μια !
Οποτε με αυτη τη προϋποθεση ΙΣΟΠΙΘΑΝΩΝ ΣΥΝΔΥΑΣΜΩΝ προκύπτει ο τυπος που χρησιμοποιειτε για τον υπολογισμο πιθανοτητας νικητη ! Χωρις την παραδοχη αυτη - πως ολοι οι συνδυασμοι πονταρισματων ειναι ισοπιθανοι - ο τυπος που χρησιμοποιειτε παει στα σκουπιδια !

Η συνήθης παραδοχή που γίνεται είναι ότι τα απλά ενδεχόμενα είναι μεταξύ τους ισοπίθανα. Ο "συνδυασμός πονταρισμάτων" όπως το (1,1,1) είναι μία περίπτωση στις συνολικές δυνατές περιπτώσεις, άρα απλό ενδεχόμενο. Το (1,2,3) είναι κι αυτό μια περίπτωση στις συνολικές δυνατές, για αυτό υπάρχει ο όρος απλό ενδεχόμενο. Στο λύκειο που οι περιπτώσεις είναι πεπερασμένου αριθμού, μαζεύουμε όλα τα απλά ενδεχόμενα στο σύνολο Ω. Αν δεν έχουμε κάποιο λόγο να αποδώσουμε άνισες πιθανότητες, κατανέμουμε την ίδια πιθανότητα.

ακριβως ! ΑΝ ΔΕΝ εχουμε καποιο λογο !

Στη περιπτωση ΤΩΡΑ του τζοκερ, το πονταρισμα ειναι η στηλη η οποια αποτελειται ΟΧΙ απο εναν αριθμο αλλα απο 5 + 1 αριθμους ! Και η επιλογη αυτων των 5+1 αριθμων για καθε συμμετασχοντα παιχτη ΔΕΝ γινεται τυχαια απο μια κληρωτιδα, αλλα την φτιαχνει Ο ΙΔΙΟΣ ο παιχτης ! Επειδη λοιπον τη φτιαχνει ο ιδιος ο παιχτης, προσπαθωντας να μιμηθει την τυχη, εξαιρει ΑΥΤΟΜΑΤΑ όλες τις 5αδες που εχουν οποιοδηποτε μαθηματικο ή γεωμετρικο πατερν !

Εδώ ξεφεύγουμε από τις πιθανότητες. Αυτό είναι μια θεωρία συμπεριφοράς για το πώς νομίζεις ότι παίζουν οι παίκτες. Αν η βάση της θεωρίας είναι να "μιμηθούν την τύχη" αποφεύγοντας αυτά που εκείνοι αναγνωρίζουν για "πάτερν", αφενός διαφωνώ, για το τι αντιλαμβάνονται ως "τυχαίο" και τι όχι. Αφετέρου θα θυμηθώ παλιές μου αναμνήσεις που έπαιζα και υπήρχαν έτοιμα να αγοράσεις, συμπληρωμένα δελτία εκτυπωμένα από μηχανή, ακριβώς με στήλες "γεωμετρικά φτιαγμένες" σαν κι αυτές που ισχυρίζεσαι πως αποφεύγουν:

Αυτο σημαινει πως σε 5 εκ παιγμενες στηλες ΔΕΝ ΘΑ ΕΜΦΑΝΙΣΤΟΥΝ ΠΟΤΕ 100 ιδιες ή 1000 ιδιες ή 1 εκ ιδιες στηλες με αριθμους :

1,2,3,4,5 + τζοκερ 6 ή
2,4,6,8,10 + τζοκερ 12 ή
3,6,9,12,15 + τζοκερ 18
κοκ

Ακομα κι αν καποιος παιξει μια δυο τετοιου τυπου στηλες ΔΕΝ θα δεις ποτε αυτες τις στηλες να επαναλαμβανονται 100 ή 150 ή 1000, ή 2 εκ φορες μεσα στις 5 εκ παιγμενες στηλες ! ΠΟΤΕ !

Εγώ νομίζω ότι θα βρεις πολλούς να παίζουν γνώριμα αριθμητικά ή γεωμετρικά μοτίβα από τη ζωή τους, π.χ. το τηλέφωνό τους, την ημερομηνία γέννησης, ή να σχεδιάζουν γραμμές και καρδούλες με τη διάταξη των αριθμών πάνω στο χάρτινο δελτίο. Κάθε παίκτης έχει διαφορετικές αντιλήψεις για προτιμητέες και αποφευκτέες στήλες. Επιπλέον, σε αυτό που θα προτιμήσει ή θα αποφύγει ο ένας παίκτης, ο άλλος παίκτης θα κάνει το ανάποδο, δηλαδή το ποντάρισμα ανακατεύεται.

Το αποτέλεσμα της κληρωτίδας είναι αυτό που θα πρέπει να μαντέψουν οι παίκτες. Η κληρωτίδα όμως δεν έχει προτιμήσεις οπότε ένα αποτέλεσμα όπως το 1,2,3,4,5 + τζόκερ 6 είναι εξίσου πιθανό όσο κάθε άλλο μέσα στα 24.435.180 δυνατά αποτελέσματα. (Ώσπου ένας κορυφαίος φυσικός μας δείξει πώς η κλήρωση γίνεται πιο προβλέψιμη, αν και μάλλον θα λαμβάνει υπόψη ακόμη και το 3ο δεκαδικό ψηφίο από τον πυρετό αυτουνού που πατάει το κουμπί για την έναρξη της κλήρωσης ).

Κι αφού η κληρωτίδα δεν έχει προτιμήσεις, οι παίκτες πιέζονται να προσαρμοστούν σε αυτό και να κάνουν πιο ανοιχτόμυαλα τις επιλογές τους σε στήλες, παρά να τις βρίσκουν γρουσούζες.

Και εν τέλει, πόσες πια είναι αυτές οι στήλες τζόκερ που ισχυρίζεσαι ότι όλοι οι παίκτες αποφεύγουν να παίξουν; Εκατό χιλιάδες; Πεντακόσιες χιλιάδες; Με ποιο σκεπτικό είναι στατιστικά σημαντικό;

Ωστοσο ο τυπος που χρησιμοποιειτε εσεις θεωρει πως ολες αυτες οι επαναλαμβανομενες στηλες θα εμφανιστουν 100, 150, 1000, 1εκ κλπ φορες μεσα στα 5 εκ παιγμενων στηλων ΜΕ ΤΗΝ ΙΔΙΑ ΑΚΡΙΒΩΣ πιθανοτητα που θα εμφανιστουν και ολοι οι υπολοιποι συνδυασμοι !

Αυτην την αστοχια, ερχονται στη πραγματικοτητα και την λυνουν οι κατανομες πιθανοτητων που ειναι ανομοιομορφες και ΑΠΑΓΟΡΕΥΟΥΝ στους συνδυασμους να ειναι ισοπιθανοι ! Δηλ. μεγενθυνουν την πιθανοτητα σε μια περιοχη συνδυασμων και εξαφανιζουν την πιθανοτητα απο μια αλλη περιοχη συνδυασμων ! Με λιγα οι κατανομες πιθανοτητων πανε και ΥΠΟΘΕΤΟΥΝ ΕΥΣΤΟΧΑ ποσες ειναι διπλες τριπλες κλπ στηλες στα 5εκ παιγμενων στηλων !

Όχι, με κάποια άλλη κατανομή πιθανοτήτων δεν ξεπερνάς την αστοχία. Δεν έχεις καν μια εξήγηση για το ποιες "περιοχές συνδυασμών" πρέπει να αποκτήσουν καλύτερες πιθανότητες από τις άλλες, προκειμένου να επιλέξεις μια "κατανομή πιθανοτήτων" (που οι καθιερωμένες κάνουν μετατροπές της ομοιόμορφης κατανομής, πηγαίνοντας από την μια τυχαία μεταβλητή στην άλλη). Εξήγηση πάντως δεν είναι να μου φέρεις μια υποκειμενική αντίληψη για τη συμπεριφορά ενός συνόλου παικτών.

Σε τέτοιες περιπτώσεις παίρνεις τα εμπειρικά δεδομένα του παρελθόντος, συγκεντρώνεις δηλαδή τις κατά μέσο όρο 3-4 εκατομμύρια στήλες ανά παιχνίδι, που έχουν παιχθεί από τους παίκτες στο παρελθόν, για να αναλύσεις στατιστικά αν υπάρχουν σημαντικές μεροληψίες υπέρ κάποιων στηλών, για να βρεις ποιες προτιμάει και ποιες αποφεύγει να παίζει... και μετά; Μετά θα σχηματίσεις ένα κατά πολύ βελτιωμένο ενδεχόμενο του Α, που έχει ακριβέστερη τη συχνότητα των 24.435.180 δυνατών επιλογών; Και τι θα κάνεις με αυτό, θα υπολογίσεις καλύτερη πιθανότητα να βρεθεί νικητής, σύμφωνα με τη θεωρία σου για τη συμπεριφορά των παικτών τζόκερ;

Θέλω να σε δω να τραβάς τέτοια ζόρια.

Μαν δυστυχως για σενα σε αυτο το κομματι τα επιχειρηματα ειναι ΟΛΑ υπερ μου ! Και το λεω χωρις κανενα ιχνος επιθετικοτητας ή υπεροψιας, ισα ισα που εκτιμω οτι εχεις μεινει να το παλευεις εσυ, ενω οι λαλιστατοι προφεσοροι με πτυχιο γκουγκλ εξαφανιστηκαν !

Χωρις να κανω σκιπ τα παραπανω που μου γραφεις θα παω σε ενα συντριπτικο επιχειρημα που εως τωρα δεν εχω αναφερει και το οποιο καταρριπτει εντελως τον μαθηματικο τυπο σας στο πραγματικο τζοκερ, Δηλ. με αυτο που θα πω τωρα σημαινει πως στο πραγματικο τζοκερ ο τυπος σας και το ai που τον βγαζει ΕΙΝΑΙ ΛΑΘΟΣ !

Ο μαθηματικος σας τυπος θεωρει οτι οι 5 εκ παιγμενες στηλες ειναι απο 5 εκ διαφορετικους παικτες οι οποιοι επειδη ειναι διαφορετικοι ειναι και ανεξαρτητοι μεταξυ τους οπως ειδαμε στο παραδειγμα με τη ζαρια ! Δηλ. θεωρει πως καθε παικτης παιζει ΜΙΑ ΣΤΗΛΗ ! ΑΜ ΔΕ !

Οι παικτες ΔΕΝ ΕΙΝΑΙ ΙΣΟΙ με τις παιγμενες στηλες ! Τι σημαινει αυτο ? Αυτο σημαινει οτι αποκλειεται ο ιδιος παικτης να παιξει 2 ή 3 ή 4 ή 5 κλπ ΙΔΙΕΣ ΣΤΗΛΕΣ, ΟΠΟΙΑ 6ΑΔΑ ΑΡΙΘΜΩΝ ΑΠΟ ΤΙΣ 24 ΕΚ ΔΥΝΑΤΕΣ ΕΞΑΔΕΣ, ΚΙ ΑΝ ΕΧΕΙ ΚΑΘΕ ΜΙΑ ΑΠΟ ΑΥΤΕΣ ΤΙΣ ΣΤΗΛΕΣ ! Αρα απευθειας εξαφανιστηκαν δισεκατομμυρια συνδυασμοι στους οποιους ο μαθηματικος σας τυπος αποδιδει κανονικα πιθανοτητα εμφανισης !

Να το δουμε με ενα μαθηματικο παραδειγμα : Αν τα 5 εκ στηλες παιχτηκαν απο 3 εκ παικτες, αυτο σημαινει πως για καθε ενα απο τα 24 εκ δυνατων συνδυασμων 5+1, δεν προκειται να εμφανιστουν ΠΟΤΕ πανω απο 3 εκ ΙΔΙΕΣ στηλες ! Ο μαθηματικος σας τυπος αποδιδει πιθανοτητα εμφανισης και για 3 εκ. ιδιες στηλες + 1, 3 εκ. ιδιες στηλες + 2, 3 εκ. ιδιες στηλες + ν ... και αυτο το κανει για καθε μια απο τις 24 εκ δυνατες 6αδες τζοκερ !
Μιλαμε για δισεκατομμυρια δισεκατομμυριων συνδυασμων που απευθειας εξαφανιζονται στο πραγματικο τζοκερ, και στους οποιους ο μαθηματικος σας τυπος αποδιδει πιθανοτητα εμφανισης χωρις αυτοι να υπαρχουν στο πειραμα !

Μετα απο αυτο που μολις ειπα κανονικα η συζητηση για το αν ισχυει ο τυπος σας πρεπει να σταματησει ! ΔΕΝ ΙΣΧΥΕΙ !

ΥΓ Ελπιζω να μην προσπαθησεις να με πεισεις οτι καθε ενας απο τα 3 εκ διαφορετικων παιχτων παιζουν ιδιες στηλες !
___________________________________________

Τωρα μονο και μονο για την ιστορια, οι κατανομες πιθανοτητων εφευρεθηκαν για να περιγραψουν αυτο που ειπες πιο πανω ΣΥΜΠΕΡΙΦΟΡΕΣ, δηλ. ΠΡΟΤΙΜΗΣΕΙΣ της τυχης ! Το θεμα δεν ειναι αν 2,3,5 παιχτες επιλεξουν με ή χωρις πατερν 5+1 αριθμους ! Το θεμα ειναι αν ΜΕ ΤΟ ΙΔΙΟ ΠΑΤΕΡΝ εμφανιστουν 2 εκ στηλες, 3 εκ στηλες, 4.355.121 στηλες κλπ γιατι σε ολους αυτους τους συνδυασμους ο μαθηματικος σας τυπος ΑΠΟΔΙΔΕΙ κανονικα ΠΙΘΑΝΟΤΗΤΑ ΕΜΦΑΝΙΣΗΣ, ενω αυτα ειναι ενδεχομενα που ΔΕΝ ΜΕΤΕΧΟΥΝ ΣΤΟ ΠΕΙΡΑΜΑ ! Δεν προκειται ποτε πανω απο 100-200 ανθρωποι να παιξουν το ΙΔΙΟ πατερν !

Μιας και το ρωτας, ο τροπος που λειτουργει η εφαρμογη μιας κατανομης πιθανοτητας ειναι με στατιστικη επεξεργασια των στηλων που παιχτηκαν για ενα χ διαστημα, στο οποιο θα μου πεις σωστα οτι δεν εχουμε προσβαση, αρα δεν μπορουμε να χρησιμοποιησουμε κατανομη πιθανοτητας ! Αρα επειδη δεν εχουμε προσβαση ο μαθηματικος σας τυπος τις θεωρει λανθασμενα ολες ισοπιθανες, περιγραφοντας αλλο πειραμα !

Ποιο πειραμα ? Το πειραμα στο οποιο καθε στηλη που παιζεται ΔΕΝ συμπληρωνεται απο ανθρωπο, αλλα βγαινει απο κληρωτιδα ! Τι ειναι αυτο ? Το λαχειο !

Ο μαθηματικος σας τυπος περιγραφει τη λοταρια, οχι το τζοκερ !

___________________________________

Συνοψίζοντας και κλεινοντας :

Ο μαθηματικος τυπος 1 - (1-(1/24.435.180)^πληθος στηλων) που χρησιμοποιειτε για να υπολογισετε πιθανοτητα νικητη, ΔΕΝ ΙΣΧΥΕΙ γιατι προϋποθετει :

1) πως καθε παιχτης παιζει ΑΚΡΙΒΩΣ ΜΙΑ ΣΤΗΛΗ το οποιο δεν ισχυει στο πραγματικο τζοκερ και

2) πως η ΜΟΝΑΔΙΚΗ στηλη που παιζει ο καθε παικτης προκυπτει απο εντελως τυχαια κληρωτιδα που και παλι δεν ισχυει στο πραγματικο τζοκερ.


Απο τα παραπανω εξαγεται πως στην πραγματικοτητα οι πολλαπλα εμφανιζομενες στηλες ειναι πολυ λιγες !

[Ανίκητος]

Μαν δυστυχως για σενα σε αυτο το κομματι τα επιχειρηματα ειναι ΟΛΑ υπερ μου ! Και το λεω χωρις κανενα ιχνος επιθετικοτητας ή υπεροψιας, ισα ισα που εκτιμω οτι εχεις μεινει να το παλευεις εσυ, ενω οι λαλιστατοι προφεσοροι με πτυχιο γκουγκλ εξαφανιστηκαν !

Χωρις να κανω σκιπ τα παραπανω που μου γραφεις θα παω σε ενα συντριπτικο επιχειρημα που εως τωρα δεν εχω αναφερει και το οποιο καταρριπτει εντελως τον μαθηματικο τυπο σας στο πραγματικο τζοκερ, Δηλ. με αυτο που θα πω τωρα σημαινει πως στο πραγματικο τζοκερ ο τυπος σας και το ai που τον βγαζει ΕΙΝΑΙ ΛΑΘΟΣ !

Ο μαθηματικος σας τυπος θεωρει οτι οι 5 εκ παιγμενες στηλες ειναι απο 5 εκ διαφορετικους παικτες οι οποιοι επειδη ειναι διαφορετικοι ειναι και ανεξαρτητοι μεταξυ τους οπως ειδαμε στο παραδειγμα με τη ζαρια ! Δηλ. θεωρει πως καθε παικτης παιζει ΜΙΑ ΣΤΗΛΗ ! ΑΜ ΔΕ !

Δεν έχει γίνει κάποια υπόθεση για τους παίκτες που συμμετέχουν στο τζόκερ, αλλά για τις στήλες που καταθέτουν συγκεντρωτικά. Και όταν λες ότι οι παίκτες είναι ανεξάρτητοι μεταξύ τους, καταλαβαίνω ότι εννοείς πως δεν συνεννοούνται μεταξύ τους για το ποιες στήλες θα υποβάλουν. Η ανεξαρτησία των παικτών εξασφαλίζει την ανεξαρτησία των επιλεγμένων στηλών που συγκεντρώνονται πριν από την κλήρωση.

Μπορείς να ανατρέξεις στους δυο πίνακες για να δεις πώς εγώ αντιλαμβάνομαι το παιχνίδι. Δεν τοποθετώ πουθενά το ποιος παίκτης έστειλε ποια στήλη.

Οι παικτες ΔΕΝ ΕΙΝΑΙ ΙΣΟΙ με τις παιγμενες στηλες ! Τι σημαινει αυτο ? Αυτο σημαινει οτι αποκλειεται ο ιδιος παικτης να παιξει 2 ή 3 ή 4 ή 5 κλπ ΙΔΙΕΣ ΣΤΗΛΕΣ, ΟΠΟΙΑ 6ΑΔΑ ΑΡΙΘΜΩΝ ΑΠΟ ΤΙΣ 24 ΕΚ ΔΥΝΑΤΕΣ ΕΞΑΔΕΣ, ΚΙ ΑΝ ΕΧΕΙ ΚΑΘΕ ΜΙΑ ΑΠΟ ΑΥΤΕΣ ΤΙΣ ΣΤΗΛΕΣ ! Αρα απευθειας εξαφανιστηκαν δισεκατομμυρια συνδυασμοι στους οποιους ο μαθηματικος σας τυπος αποδιδει κανονικα πιθανοτητα εμφανισης !

Μπορεί ο ένας παίκτης να μην παίξει την ίδια στήλη παραπάνω από δυο φορές. Ωστόσο υπάρχει η περίπτωση πολλοί παίκτες να παίξουν συμπτωματικά την ίδια στήλη. Όταν συγκεντρωθούν όλες οι στήλες, η στήλη που έπαιξαν εκείνοι οι παίκτες θα εμφανίζεται επαναλαμβανόμενη.

Να το δουμε με ενα μαθηματικο παραδειγμα : Αν τα 5 εκ στηλες παιχτηκαν απο 3 εκ παικτες, αυτο σημαινει πως για καθε ενα απο τα 24 εκ δυνατων συνδυασμων 5+1, δεν προκειται να εμφανιστουν ΠΟΤΕ πανω απο 3 εκ ΙΔΙΕΣ στηλες ! Ο μαθηματικος σας τυπος αποδιδει πιθανοτητα εμφανισης και για 3 εκ. ιδιες στηλες + 1, 3 εκ. ιδιες στηλες + 2, 3 εκ. ιδιες στηλες + ν ... και αυτο το κανει για καθε μια απο τις 24 εκ δυνατες 6αδες τζοκερ !
Μιλαμε για δισεκατομμυρια δισεκατομμυριων συνδυασμων που απευθειας εξαφανιζονται στο πραγματικο τζοκερ, και στους οποιους ο μαθηματικος σας τυπος αποδιδει πιθανοτητα εμφανισης χωρις αυτοι να υπαρχουν στο πειραμα !

Με συγχωρείς, αλλά έχεις διαβάσει μια προηγούμενη απάντηση;
Ανίκητος @ Τα τυχερά παιχνίδια είναι στημένα

Σε εκείνη την απάντηση, έγραψα ότι οι δυνατοί τρόποι για να συγκεντρώσεις ένα σύνολο 48 εκατομμυρίων στηλών είναι (24435180)^^48000000 και το συμβόλισα Ν(Ω_|48000000|).

Ομοίως οι δυνατοί τρόποι με τους οποίους συγκεντρώνονται 5 εκατομμύρια στήλες, είναι Ν(Ω)=(24435180)^^5000000 (ας μη βάλω το |5000000| δείκτη στο Ω).

Ο μαθηματικός τύπος "μας" αναφέρει ότι αυτό το Ν(Ω) πηγαίνει στον παρονομαστή οποτεδήποτε θες να υπολογίσεις την πιθανότητα να εμφανιστεί ένας συγκεκριμένος "συνδυασμός" από 5 εκατομμύρια στήλες.

Δίνεις το παράδειγμα ενός "συνδυασμού" που ισχυρίζεσαι ότι αποκλείεται να εμφανιστεί, με 3 εκατομμύρια ίδιες στήλες μέσα στις 5 εκατομμύρια συγκεντρωμένες. Αυτό είναι ένα ενδεχόμενο Β που μπορεί να εμφανιστεί με Ν(Β)=(24435180)^^2000001 τρόπους, άρα έχει πιθανότητα:

P(Β)=N(A)/N(Ω) = 1 / (24435180)^^2999999

η οποία μου φαίνεται αρκετά κοντά στο μηδέν. Είναι στατιστικά σημαντική η διαφορά αυτής της πιθανότητας από το απόλυτο μηδέν που εσύ ισχυρίζεσαι; Οπότε συμφωνώ, για ίσως διαφορετικούς λόγους από σένα, ότι αποκλείεται να εμφανιστεί αυτό το παράδειγμα που δίνεις. Ο μαθηματικός μου τύπος το επιβεβαιώνει.

Επιπρόσθετα, σαν σχόλιό μου στην αντίληψη που έχεις για τη συμπεριφορά των παικτών, η πιθανότητα μηδέν να προσέλθουν 5 εκατομμύρια παίκτες ώστε να συγκεντρωθούν 3 εκατομμύρια ίδιες στήλες στο ποντάρισμά τους, σημαίνει ότι αποκλείεις την ικανότητά τους να το κάνουν, κατά κάποιο τρόπο θα εκβιαστούν ή θα πεθάνουν οι παίκτες μόλις συγκεντρωθούν στο ίδιο σημείο τα 3 εκατομμύρια ίδιες στήλες.

Σε ξαναρώτησα, πόσες εν τέλει είναι οι "δισεκατομμύρια δισεκατομμυρίων" των "συνδυασμών" του τζόκερ που πρέπει να έχουν οπωσδήποτε πιθανότητα μηδέν για να ικανοποιηθείς; Ακόμη και "τρισεκατομμύρια τρισεκατομμυρίων" να είναι, δεν είναι αρκετά σημαντικές για να μην ισχύει η χρήση του μαθηματικού τύπου P(A)=N(A)/N(Ω) που θεωρεί τα απλά ενδεχόμενα εντός του Α ισοπίθανα.

Μετα απο αυτο που μολις ειπα κανονικα η συζητηση για το αν ισχυει ο τυπος σας πρεπει να σταματησει ! ΔΕΝ ΙΣΧΥΕΙ !

ΥΓ Ελπιζω να μην προσπαθησεις να με πεισεις οτι καθε ενας απο τα 3 εκ διαφορετικων παιχτων παιζουν ιδιες στηλες !
___________________________________________

Δεν χρειάζεται.

Ποιο πειραμα ? Το πειραμα στο οποιο καθε στηλη που παιζεται ΔΕΝ συμπληρωνεται απο ανθρωπο, αλλα βγαινει απο κληρωτιδα ! Τι ειναι αυτο ? Το λαχειο !

Λάθος, γιατί στο τζόκερ μπορούν να αγοράσουν πολλοί παίκτες τον ίδιο "λαχνό" (στήλη) και στο λαχείο μόνο ένας αγοράζει έναν λαχνό με συγκεκριμένο αριθμό.

[Ανίκητος]

Συνοψίζοντας και κλεινοντας :

Ο μαθηματικος τυπος 1 - (1-(1/24.435.180)^πληθος στηλων) που χρησιμοποιειτε για να υπολογισετε πιθανοτητα νικητη, ΔΕΝ ΙΣΧΥΕΙ γιατι προϋποθετει :
1) πως καθε παιχτης παιζει ΑΚΡΙΒΩΣ ΜΙΑ ΣΤΗΛΗ το οποιο δεν ισχυει στο πραγματικο τζοκερ και

Ο τύπος δεν υπολογίζει ακριβώς την πιθανότητα ενός παίκτη να είναι νικητής, αλλά την πιθανότητα μιας παιγμένης στήλης να είναι "νικήτρια" δηλαδή να ταιριάζει με το αποτέλεσμα της κληρωτίδας του διοργανωτή. Έτερον εκάτερον ότι τουλάχιστον μια παιγμένη στήλη έχει υποβληθεί από κάθε παίκτη και άρα στους συμμετέχοντες παίκτες βρίσκεται και ο νικητής.

2) πως η ΜΟΝΑΔΙΚΗ στηλη που παιζει ο καθε παικτης προκυπτει απο εντελως τυχαια κληρωτιδα που και παλι δεν ισχυει στο πραγματικο τζοκερ.

Κάθε παίκτης παίζει μαντεύοντας το αποτέλεσμα της κληρωτίδας του παιχνιδιού. Δεν χρειάζεται για αυτό δική του κληρωτίδα.

Απο τα παραπανω εξαγεται πως στην πραγματικοτητα οι πολλαπλα εμφανιζομενες στηλες ειναι πολυ λιγες !

Άρα ένας λόγος παραπάνω να ισχύει ο μαθηματικός τύπος που απέρριψες.

[ΠΑΓΧΡΗΣΤΟΣ]

Υπάρχει κόσμος που παίζει τυχερά παιχνίδια;
Απορία ψάλτου βηξ

[Ανίκητος]

Υπάρχει κόσμος που παίζει τυχερά παιχνίδια;
Απορία ψάλτου βηξ

Αν ήταν όλοι έτσι εγκρατείς, δεν θα αναπτυσσόταν η θεωρία πιθανοτήτων ποτέ.

[micmic]

Υπάρχει κόσμος που παίζει τυχερά παιχνίδια;
Απορία ψάλτου βηξ

Ε, τώρα που είχε τζόκερ 20 μύρια (16 μετά φόρων) θα μπορούσε να συμφέρει. Δίνεις 13 εκ και παίζεις 13 εκ στήλες (πάνω από 50% πιθανότητες να πιάσεις τη νικήτρια στήλη) και αν είσαι ο μοναδικός νικητής βγάζεις 3 εκ. Άσχημα είναι αυτές οι πιθανότητες για 3 εκ κέρδος;

[nik_killthemall]

Μαν δυστυχως για σενα σε αυτο το κομματι τα επιχειρηματα ειναι ΟΛΑ υπερ μου ! Και το λεω χωρις κανενα ιχνος επιθετικοτητας ή υπεροψιας, ισα ισα που εκτιμω οτι εχεις μεινει να το παλευεις εσυ, ενω οι λαλιστατοι προφεσοροι με πτυχιο γκουγκλ εξαφανιστηκαν !

Χωρις να κανω σκιπ τα παραπανω που μου γραφεις θα παω σε ενα συντριπτικο επιχειρημα που εως τωρα δεν εχω αναφερει και το οποιο καταρριπτει εντελως τον μαθηματικο τυπο σας στο πραγματικο τζοκερ, Δηλ. με αυτο που θα πω τωρα σημαινει πως στο πραγματικο τζοκερ ο τυπος σας και το ai που τον βγαζει ΕΙΝΑΙ ΛΑΘΟΣ !

Ο μαθηματικος σας τυπος θεωρει οτι οι 5 εκ παιγμενες στηλες ειναι απο 5 εκ διαφορετικους παικτες οι οποιοι επειδη ειναι διαφορετικοι ειναι και ανεξαρτητοι μεταξυ τους οπως ειδαμε στο παραδειγμα με τη ζαρια ! Δηλ. θεωρει πως καθε παικτης παιζει ΜΙΑ ΣΤΗΛΗ ! ΑΜ ΔΕ !

Δεν έχει γίνει κάποια υπόθεση για τους παίκτες που συμμετέχουν στο τζόκερ, αλλά για τις στήλες που καταθέτουν συγκεντρωτικά. Και όταν λες ότι οι παίκτες είναι ανεξάρτητοι μεταξύ τους, καταλαβαίνω ότι εννοείς πως δεν συνεννοούνται μεταξύ τους για το ποιες στήλες θα υποβάλουν.

Μαν ο μαθηματικος σας τυπος, προϋποθετει ότι το αν και ποσες στήλες εμφανίζονται πολλαπλά είναι κρυφό στον παρατηρητή ! Αυτό μαθηματικώς οδηγεί στην ανεξαρτησία της καθε στήλης που οδηγεί με τη σειρά του στον μαθηματικό σας τύπο !

Από τη στιγμή όμως που ο καθε παρατηρητής γνωρίζει πως κάθε παίχτης μπορεί να παίξει πανω απο 1 στήλη, αυτόματα στον παρατηρητή είναι ορατό ότι ο κάθε παίχτης ΔΕΝ υπαρχει περίπτωση να παίξει ΙΔΙΕΣ στηλες 2,3,4, ν ΙΔΙΕΣ στηλες, αρα χαθηκε η ανεξαρτησια, οπότε χαθηκε η ισχυς του μαθηματικου σας τυπου !

Δηλ. ΔΕΝ αποδεικνυεται ΜΑΘΗΜΑΤΙΚΩΣ ο τυπος σας για το συγκεκριμενο παιχνιδι και η πιστη σε αυτον ειναι θρησκευτικου τυπου δηλ ανευ αποδειξης.

Δίνεις το παράδειγμα ενός συνδυασμού που ισχυρίζεσαι ότι αποκλείεται να εμφανιστεί, με 3 εκατομμύρια ίδιες στήλες μέσα στις 5 εκατομμύρια συγκεντρωμένες. Αυτό είναι ένα ενδεχόμενο Β που μπορεί να εμφανιστεί με Ν(Β)=(24435180)^^2000001 τρόπους, άρα έχει πιθανότητα:

P(Β)=N(A)/N(Ω) = 1 / (24435180)^^2999999

η οποία μου φαίνεται αρκετά κοντά στο μηδέν. Είναι στατιστικά σημαντική η διαφορά αυτής της πιθανότητας από το απόλυτο μηδέν που εσύ ισχυρίζεσαι; Οπότε συμφωνώ, για ίσως διαφορετικούς λόγους από σένα, ότι αποκλείεται να εμφανιστεί αυτό το παράδειγμα που δίνεις. Ο μαθηματικός μου τύπος το επιβεβαιώνει.

Επιπρόσθετα, σαν σχόλιό μου στην αντίληψη που έχεις για τη συμπεριφορά των παικτών, η πιθανότητα μηδέν να προσέλθουν 5 εκατομμύρια παίκτες ώστε να συγκεντρωθούν 3 εκατομμύρια ίδιες στήλες στο ποντάρισμά τους, σημαίνει ότι αποκλείεις την ικανότητά τους να το κάνουν, κατά κάποιο τρόπο θα πεθάνουν οι παίκτες μόλις συγκεντρωθούν στο ίδιο σημείο τα 3 εκατομμύρια ίδιες στήλες.

Αυτο που λες εδω ειναι σωστο, τοση ειναι η πιθανοτητα που χανεται, ΣΤΟ ΠΡΩΤΟ απο τα δυο διαδοχικα πειραματα, αλλα δεν συνεχιζεις τη σκεψη σου οποτε ΔΕΝ βλεπεις την ΜΕΓΑΛΗ αστοχια !

Δωσε βαση :

Αν λοιπον στις 5 εκ στηλες οι ΔΙΑΦΟΡΕΤΙΚΟΙ παιχτες ειναι 3 εκ, τοτε αυτοματα ο τυπος υπολογισμου σας για την πιθανοτητα ΜΗ νικητη γινεται

(1-(1/24.435.180))^3000000) ΚΑΙ ΟΧΙ (1-(1/24.435.180))^5000000), γιατι αυτοματα γνωριζουμε ως παρατηρητες, πως ΔΕΝ υπαρχει περιπτωση καποιος απο τους 3 εκ παιχτες να παιξει ιδια στηλη με τον εαυτο του !

το πρωτο δινει πιθανοτητα 88,44% να μην υπαρξει νικητης και το δευτερο που ισχυριζοσασταν ως τωρα δινει πιθανοτητα 81,5% να μην υπαρξει νικητης !
Αυτη ειναι μεγαλη διαφορα !


Και τι γινεται αν τελικα στις 5εκ στηλες οι διαφορετικοι παιχτες ειναι 2,5εκ τοτε η πιθανοτητα να μην υπαρξει νικητης γινεται (1-(1/24.435.180))^2500000) = 90,2%

Με λιγα λογια μαν, η δυνατοτητα καθε παικτης να παιζει πανω απο μια στηλη ΟΔΗΓΕΙ ΣΤΗΝ ΑΠΩΛΕΙΑ ΤΗΣ ΠΛΗΡΟΦΟΡΙΑΣ που μεχρι τωρα νομιζατε οτι γνωριζατε "ποσες στηλες παιχτηκαν" ! Στον τυπο σας δεν χρειαζεστε τις στηλες που παιχτηκαν αλλα ΤΟΥΣ ΔΙΑΦΟΡΕΤΙΚΟΥΣ παιχτες που επαιξαν, που αυτο ΔΕΝ ΤΟ ΓΝΩΡΙΖΕΤΕ αρα δεν μπορει να εφαρμοστει ο τυπος σας.

Και δεν μπορει να εφαρμοστει ο τυπος σας και για εναν ακομη λογο : Γιατι απο τη στιγμη που οι παιχτες παιζουν ΔΙΑΦΟΡΕΤΙΚΟ ΑΡΙΘΜΟ ΜΗ ΙΔΙΩΝ ΣΤΗΛΩΝ, δεν εχει ο καθε παιχτης την ιδια πιθανοτητα να χασει !

Με λιγα λογια ο μαθηματικος σας τυπος ειναι μη εφαρμοσιμος, νοτ απλικαμπλ που λενε !

Προφανως λογω γκουγκλ γνωσης ο προφεσορος που εφερε τον τυπο στο νημα δεν γνωριζε οτι ο τυπος αυτος δουλευει με ανεξαρτητα παιξιματα απο διαφορετικους παιχτες !

Ποιο πειραμα ? Το πειραμα στο οποιο καθε στηλη που παιζεται ΔΕΝ συμπληρωνεται απο ανθρωπο, αλλα βγαινει απο κληρωτιδα ! Τι ειναι αυτο ? Το λαχειο !

Λάθος, γιατί στο τζόκερ μπορούν να αγοράσουν πολλοί παίκτες τον ίδιο "λαχνό" (στήλη) και στο λαχείο μόνο ένας αγοράζει έναν λαχνό.

Εδω, εχεις δικιο, αλλα οχι γιαυτο που λες, γιατι και στο λαχειο μπορει ο ιδιος παιχτης να αγορασει 2,3,4 λαχεια !
Εχεις δικιο γιατι στο λαχειο ΔΕΝ υπαρχουν ΙΔΙΟΙ ΛΑΧΝΟΙ αλλα ολοι ειναι διαφορετικοι

αρα ο μαθηματικος σας τυπος δεν περιγραφει τπτ ουτε το τζοκερ ουτε το λαχειο εντελως κουβα

ΥΓ το βραδακι θα σου τρεξω αναλυτικα το αναλογο του μαο μαο με τη ζαρια και τους 3 πχωρουμιτες οι οποιοι ομως θα μπορουν να κανουν πανω απο 1 πονταρισμα ο καθενας π.χ 1 πονταρισμα ο ενας, 2 πονταρισματα ο δευτερος και 2 πονταρισματα ο τριτος για να δεις την αστοχια του τυπου σας και του συλλογισμου σας στο απλοποιημενο παραδειγμα.

[Ανίκητος]

Μαν ο μαθηματικος σας τυπος, προϋποθετει ότι το αν και ποσες οι στήλες εμφανίζονται πολλαπλά είναι κρυφό στον παρατηρητή ! Αυτό μαθηματικώς οδηγεί στην ανεξαρτησία της καθε στήλης που οδηγεί με τη σειρά του στον μαθηματικό σας τύπο !

Ποιον παρατηρητή; Σοβαρά τώρα;

Από τη στιγμή όμως που ο καθε παρατηρητής γνωρίζει πως κάθε παίχτης μπορεί να παίξει πανω απο 1 στήλη, αυτόματα στον παρατηρητή είναι ορατό ότι ο κάθε παίχτης ΔΕΝ υπαρχει περίπτωση να παίξει ΙΔΙΕΣ στηλες 2,3,4, ν ΙΔΙΕΣ στηλες, αρα χαθηκε η ανεξαρτησια, οπότε χαθηκε η ισχυς του μαθηματικου σας τυπου !

Δεν τέθηκε ποτέ απαγόρευση στους παίκτες να παίξουν παραπάνω από μία στήλες. Ο μαθηματικός τύπος δεν τη χρειάζεται, γιατί αναφέρεται στις παιγμένες στήλες που συγκεντρώνονται στον διοργανωτή, σε κάθε παιχνίδι.

Η ανεξαρτησία (των παικτών) σημαίνει ότι το τι θα παίξει ένας παίκτης δεν εξαρτάται από τι θα παίξουν οι υπόλοιποι. Και επειδή δεν ασχολήθηκα με παίκτες, αλλά με παιγμένες στήλες που υποβλήθηκαν από αυτούς και συγκεντρώθηκαν στο διοργανωτή, η ανεξαρτησία (των συγκεντρωμένων στηλών) σημαίνει ότι μία στήλη δεν εξαρτάται από όλες τις υπόλοιπες.

Μπορώ να καταλάβω ότι μπορεί να συμβεί στις δικές του στήλες, που έχει υποβάλει κάποιος παίκτης, να μην έχουν προκύψει με ανεξάρτητο τρόπο μέσα του, αλλά έχουν με κάποιο σκεπτικό μια δική τους αλληλεξάρτηση. Δεν αλλάζει όμως την τοποθέτησή μου για το πώς μπορεί να συμπεριφέρεται κάθε παίκτης: Ανίκητος @ Τα τυχερά παιχνίδια είναι στημένα

Η ανεξαρτησία πρακτικά σημαίνει ότι κάθε ένας τρόπος, από όλους τους τρόπους με τους οποίους μπορούν να συγκεντρωθούν οι στήλες των παικτών, αποτελούν απλά ενδεχόμενα. Εσύ αποκλείεις κάποιους τρόπους, δίνοντας μηδενική πιθανότητα σε συγκεκριμένα απλά ενδεχόμενα, το πλήθος των οποίων είναι, όπως έχεις πει, "δισεκατομμύρια δισεκατομμυρίων". Είναι λίγα.

Σε σχέση δηλαδή με τους δυνατούς τρόπους που μπορούν να συγκεντρωθούν οι παιγμένες στήλες στο διοργανωτή, δεν είναι αρκετά. Βρες πιο πολυπληθή ενδεχόμενα που να "σπάνε" πιο συστηματικά την ανεξαρτησία. Εκ των πραγμάτων αυτά θα αποκαλύπτουν περισσότερη πληροφορία για το πώς παίχθηκαν οι στήλες, που θα μεταβάλλει τον υπολογισμό της πιθανότητας του νικητή, δηλαδή δεν θα ισχύει ο μαθηματικός τύπος των αντιπαθών συνομιλητών σου.

Με άλλα λόγια, ο μαθηματικός τύπος ισχύει όχι γιατί τον επέλεξαν οι συνομιλητές σου, αλλά από τον τρόπο που διεξάγεται το παιχνίδι και ειδικότερα στο τι πληροφορία (πρέπει να) γίνεται γνωστή.

Δωσε βαση :

Αν λοιπον στις 5 εκ στηλες οι ΔΙΑΦΟΡΕΤΙΚΟΙ παιχτες ειναι 3 εκ, τοτε αυτοματα ο τυπος υπολογισμου σας για την πιθανοτητα ΜΗ νικητη γινεται

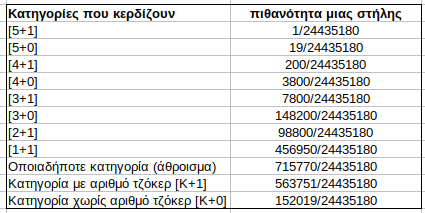
(1-(1/24.435.180))^3000000) ΚΑΙ ΟΧΙ (1-(1/24.435.180))^5000000), γιατι αυτοματα γνωριζουμε ως παρατηρητες, πως ΔΕΝ υπαρχει περιπτωση καποιος απο τους 3 εκ παιχτες να παιξει ιδια στηλη με τον εαυτο του !

το πρωτο δινει πιθανοτητα 88,44% να μην υπαρξει νικητης και το δευτερο που ισχυριζοσασταν ως τωρα δινει πιθανοτητα 81,5% να μην υπαρξει νικητης !
Αυτη ειναι μεγαλη διαφορα !

Σε τι να δώσω βάση; Σε ένα συγκεκριμένο ενδεχόμενο που έχω υπολογίσει ότι συμβαίνει με πιθανότητα 1 / (24435180)^2999999, να μην ισχύσει ο μαθηματικός τύπος;

Προφανώς αυτό το συγκεκριμένο ενδεχόμενο αποκαλύπτει την πληροφορία για το πώς παίχτηκαν οι στήλες, οπότε αλλάζει άρδην αυτά που ξέρουμε προκειμένου να υπολογίσουμε την πιθανότητα νικητή, αλλά είναι ένα ενδεχόμενο τόσο πιθανό να συμβεί, όσο η υπολογισμένη μηδαμινή πιθανότητα 1 / (24435180)^2999999

Για ποιο λόγο λοιπόν να εγκαταλείψω τον μαθηματικό τύπο, για ένα απίθανο ενδεχόμενο που θα αλλάξει άρδην τις πιθανότητες του επόμενου πειράματος τύχης, όπως το σκέφτεσαι;

Με λιγα λογια μαν, η δυνατοτητα καθε παικτης να παιζει πανω απο μια στηλη ΟΔΗΓΕΙ ΣΤΗΝ ΑΠΩΛΕΙΑ ΤΗΣ ΠΛΗΡΟΦΟΡΙΑΣ που μεχρι τωρα γνωριζατε "ποσες στηλες παιχτηκαν" !

Η μία πληροφορία που μας γίνεται διαθέσιμη από τον διοργανωτή (πόσες στήλες παίχθηκαν) για να μην πιθανολογούμε και με αυτή σε κάθε παιχνίδι, χάνεται επειδή κάποιος παίκτης έπαιξε πάνω από μια στήλη;;

Στον τυπο σας δεν χρειαζεστε τις στηλες που παιχτηκαν αλλα ΤΟΥΣ ΔΙΑΦΟΡΕΤΙΚΟΥΣ παιχτες που επαιξαν, που αυτο ΔΕΝ ΤΟ ΓΝΩΡΙΖΕΤΕ αρα δεν μπορει να εφαρμοστει ο τυπος σας.

Προφανως λογω γκουγκλ γνωσης ο προφεσορος που εφερε τον τυπο στο νημα δεν γνωριζε οτι ο τυπος αυτος δουλευει με ανεξαρτητα παιξιματα απο διαφορετικους παιχτες !

Εδώ το γυρνάς στο κλαψούρισμα.
Ο μαθηματικός τύπος μια χαρά εφαρμόζεται δεδομένων των πληροφοριών που υπάρχουν στο κάθε παιχνίδι τζόκερ.
Το να εκτοξεύεις ένα απίθανο ενδεχόμενο όπου, επειδή αποκαλύπτει περισσότερη πληροφορία για το συγκεκριμένο παιχνίδι, επηρεάζει σημαντικά την πιθανότητα για τον νικητή, δεν αλλάζει την ανάγκη του μαθηματικού τύπου, για τις αναρίθμητες υπόλοιπες περιπτώσεις που δεν υπάρχει περισσότερη πληροφορία.

[Ανίκητος]

ΥΓ το βραδακι θα σου τρεξω αναλυτικα το αναλογο του μαο μαο με τη ζαρια και τους 3 πχωρουμιτες οι οποιοι ομως θα μπορουν να κανουν πανω απο 1 πονταρισμα ο καθενας π.χ 1 πονταρισμα ο ενας, 2 πονταρισματα ο δευτερος και 2 πονταρισματα ο τριτος για να δεις την αστοχια του τυπου σας και του συλλογισμου σας στο απλοποιημενο παραδειγμα.

Δεν χρειάζεται να έρθει το βράδυ. Σ' το αναλύω και εγώ:
Στο παιχνίδι με το ζάρι των 6 εδρών, όπου 3 πχορουμίτες έχουν δικαίωμα για πάνω από ένα ποντάρισμα, η στρατηγική καθενός είναι απλή. Θα κάνουν σε κάθε ρίψη από 6 διαφορετικά πονταρίσματα (τζάμπα είναι) οπότε θα βρεθούν πάντα να είναι και οι 3 νικητές. Σε κάθε παιχνίδι.

Τα πονταρίσματα θα ανακοινώθουν 18 τον αριθμό πριν από κάθε ρίψη, για να χαθεί και η πληροφορία... με την οποία κανείς από τους τρεις πχωρουμίτες δεν θα μπορεί τάχα να επιβεβαιώσει πως ξέρει τι έπαιξε ο άλλος και θα επιμένουν ως γνήσιοι πχωρουμίτες ότι επέλεξαν τα πονταρίσματά τους ανεξάρτητα ο ένας από τον άλλο!

Ο μαθηματικός τύπος μάλιστα δίνει 1-(5/6)^18 = 0,97 δηλαδή και στην τυφλή τύχη να γίνονταν τα 6 πονταρίσματα κάθε παίκτη, πάλι θα είχαμε 97% νικητή...

Ας δούμε το ενδεχόμενο σε κάθε έδρα του ζαριού να έχουν γίνει ακριβώς 3 πονταρίσματα, από το σύνολο 18 που συγκεντρώθηκαν... Σε σχέση με όλους τους δυνατούς τρόπους που μπορούν να γίνουν τα 18 πονταρίσματα, το ενδεχόμενο αυτό έχει 1,3% πιθανότητα, με την οποία θα απορρίψουμε εύστοχα τον μαθηματικό τύπο...


____________

Προτιμώ να μου αναλύσεις τη στρατηγική καθενός σε ένα παιχνίδι, όπου έχουμε 1.000 πχορουμίτες και ένα ζάρι 24.435.180 εδρών, με όσα πονταρίσματα αντέχει η τσέπη τους (1 ευρώ έκαστο).